
【题目】小明的父亲上星期五买进某公司股票1000股,每股30元,如表为本周内每日该股票的涨跌情况(单位:元)
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 | +3 | +1.5 | -2 | -1.5 | +1 |
(1) 星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低每股多少元?
(3)已知小明父亲买进股票时付了1.5‰的手续费,卖出时需付成交额1.5‰的手续费和1‰的交易税,如果他在周五收盘前将全部股票卖出,他的收益情况如何
【答案】(1)32.5元;(2)本周内最高价是每股34.5元,最低每股31元;(3)收益将盈利1875元.
【解析】
(1)根据题意列出相应的算式,计算即可得出结果;
(2)根据表格逐个算出周一至周五每天的价格,再取最高和最低即可;
(3)分别计算出小明父亲买入股票的总价和出售股票是的总收益,作差即可得出小明父亲的盈利情况.
(1)星期三收盘时,每股价格为:30+3+1.5-2=32.5(元)
答:星期三收盘时,每股价格是32.5元.
(2)周一每股价格为:30+3=33(元)
周二每股价格为:33+1.5=34.5(元)
周三每股价格为:34.5-2=32.5(元)
周四每股价格为:32.5-1.5=31(元)
周五每股价格为:31+1=32(元)
故本周内最高价是每股34.5元,最低每股31元.
(3)小明的父亲买股票花费:![]() (元)
(元)
小明的父亲卖股票的收入为:![]() (元)
(元)
31920-30045=1875(元)
如果他在周五收盘前将全部股票卖出,他的收益将盈利1875元.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】透明的口袋里装有3个球,这3个球分别标有数字1、2、3,这些球除了数字外都相同。
(1)如果从袋中任意摸出一个球,那么摸到标有数字是2的球的概率是多少?(3分)
(2)小明和小东玩摸球游戏,游戏规则如下:先由小明随机摸出一个球,记下球的数字后放回,搅匀后再由小东随机摸出一个球,记下球的数字.谁摸出的球的数字大,谁获胜.现请你利用树状图或列表的方法分析游戏规则对双方是否公平?并说明理由。(6分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了开展阳光体育运动,某市教体局做了一个随机调查,调查内容是:每天锻炼是否超过1h及锻炼未超过1h的原因.他们随机调查了600名学生,用所得的数据制成了扇形统计图和频数分布直方图(图1、图2).

根据图示,请回答以下问题:
(1)“没时间”的人数是 ,并补全频数分布直方图;
(2)2016年该市中小学生约40万人,按此调查,可以估计2016年全市中小学生每天锻炼超过1h的约有 万人;
(3)在(2)的条件下,如果计划2018年该市中小学生每天锻炼未超过1h的人数降到7.5万人,求2016年至2018年锻炼未超过1h人数的年平均降低的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
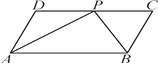
(1)求∠APB的度数;
(2)如果AD=5 cm,AP=8 cm,求△APB的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂制作甲、乙两种窗户边框,已知同样用12米材料制成甲种边框的个数比制成乙种边框的个数少1个,且制成一个甲种边框比制成一个乙种边框需要多用![]() 的材料.
的材料.
(1)求制作每个甲种边框、乙种边框各用多少米材料?
(2)如果制作甲、乙两种边框的材料共640米,要求制作乙种边框的数量不少于甲种边框数量的2倍,求应最多安排制作甲种边框多少个(不计材料损耗)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]() ,则下列结论中正确的是_____
,则下列结论中正确的是_____
①当a=5时,方程组的解是![]() ;
;
②当x,y值互为相反数时,a=20;
③当2x2y=16时,a=18;
④不存在一个实数a使得x=y.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(2,0),C(0,﹣2),直线x=m(m>2)与x轴交于点D.
(1)求二次函数的解析式;
(2)在直线x=m(m>2)上有一点E(点E在第四象限),使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似,求E点坐标(用含m的代数式表示);
(3)在(2)成立的条件下,抛物线上是否存在一点F,使得四边形ABEF为平行四边形?若存在,请求出F点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产某种产品,每件产品的生产成本为25元,出厂价为50元.在生产过程中,平均每生产一件这种产品有0.5m3的污水排出.为净化环境,该厂购买了一套污水处理设备,每处理1m3污水所需原材料费为2元,每月排污设备耗费4000元.
(1)请给出该厂每月的利润与产品件数的函数关系式;
(2)为保证每月盈利30000元,该厂每月至少需生产并销售这种产品多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com