
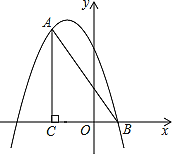
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ACB=90�㣬OC=2OB��tan��ABC=2����B������Ϊ��1��0����������y=��x2+bx+c����A��B���㣮
��1���������ߵĽ���ʽ��
��2����P��ֱ��AB�Ϸ��������ϵ�һ�㣬����P��PD��ֱx���ڵ�D�����߶�AB�ڵ�E��ʹPE=![]() DE��
DE��
�����P�����ꣻ
����ֱ��PD���Ƿ���ڵ�M��ʹ��ABMΪֱ�������Σ������ڣ�����������������е�M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=��x2��3x+4����2����P����1��6�����ڴ��ڣ�M����1��3+![]() ����1��3��
����1��3��![]() ����1����1����1��
����1����1����1��![]() ����
����
��������
��1���ȸ�����֪���A�����꣬���ô���ϵ��������κ����Ľ���ʽ��
��2�����ȵ�AB�Ľ���ʽΪ��y=-2x+2������PD��x�ᣬ��P��x��-x2-3x+4������E��x��-2x+2��������PE=![]() DE���з��̿ɵ�P�����ꣻ
DE���з��̿ɵ�P�����ꣻ
�������M�����꣬����������빫ʽ�ɵ�AB��AM��BM�ij����������������ABMΪֱ��������ʱ���ֱ���A��B��MΪֱ�Ƕ���ʱ�����ù��ɶ����з��̿ɵõ�M�����꣮
�⣺��1����B��1��0������OB=1��
��OC=2OB=2����C����2��0����
Rt��ABC��tan��ABC=2��
��![]() �� ��
�� ��![]() �� ��AC=6��
�� ��AC=6��
��A����2��6����
��A����2��6����B��1��0������y=��x2+bx+c�ã�![]() ��
��
��ã�![]() ��
��
�������ߵĽ���ʽΪ��y=��x2��3x+4��
��2���١�A����2��6����B��1��0����
��AB�Ľ���ʽΪ��y=��2x+2��
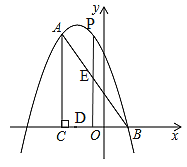
��P��x����x2��3x+4������E��x����2x+2����
��PE=![]() DE��
DE��
�ੁx2��3x+4������2x+2��=![]() ����2x+2����
����2x+2����
��x=-1��1���ᣩ��
��P����1��6����
�ڡ�M��ֱ��PD�ϣ���P����1��6����
��M����1��y����
��B��1��0����A����2��6��
��AM2=����1+2��2+��y��6��2=1+��y��6��2��
BM2=��1+1��2+y2=4+y2��
AB2=��1+2��2+62=45��
�����������
i������AMB=90��ʱ����AM2+BM2=AB2��
��1+��y��6��2+4+y2=45��
��ã�y=3![]() ��
��
��M����1��3+![]() ����1��3��
����1��3��![]() ����
����
ii������ABM=90��ʱ����AB2+BM2=AM2��
��45+4+y2=1+��y��6��2�� ��y=��1��
��M����1����1����
iii������BAM=90��ʱ����AM2+AB2=BM2��
��1+��y��6��2+45=4+y2�� ��y=![]() ��
��
��M����1��![]() ����
����
������������M����������M����1��3+![]() ����1��3��
����1��3��![]() ����1����1����1��
����1����1����1��![]() ����
����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������۹�˾��2019���һ��������![]() ����Ʒ�ƵĽ��Ĺ�126����
����Ʒ�ƵĽ��Ĺ�126����![]() ��Ʒ�ƵĽ����ۼ�Ϊÿ��6000Ԫ��
��Ʒ�ƵĽ����ۼ�Ϊÿ��6000Ԫ��![]() ��Ʒ�ƵĽ����ۼ�Ϊÿ��9000Ԫ.
��Ʒ�ƵĽ����ۼ�Ϊÿ��9000Ԫ.
��1���������۹�˾�ڵ�һ�����������ֽ��ĺ������۶����96.6��Ԫ������������![]() ��Ʒ�ƵĽ��Ķ��ټ���
��Ʒ�ƵĽ��Ķ��ټ���
��2�������۹�˾������2019��ڶ����ȵ����۸�![]() ��Ʒ�ƵĽ�������һ�����ȵĻ������µ�
��Ʒ�ƵĽ�������һ�����ȵĻ������µ�![]() ��
��![]() ��Ʒ�ƵĽ�������һ�����ȵĻ���������
��Ʒ�ƵĽ�������һ�����ȵĻ���������![]() ��ͬʱ���루1������������۶����������ȣ�
��ͬʱ���루1������������۶����������ȣ�![]() ��Ʒ�ƵĽ��ĵ�������������
��Ʒ�ƵĽ��ĵ�������������![]() ��
��![]() ��Ʒ�ƵĽ��ĵ�������������
��Ʒ�ƵĽ��ĵ�������������![]() �����2019��ڶ����ȵ����۶�ȣ�1������������۶�����
�����2019��ڶ����ȵ����۶�ȣ�1������������۶�����![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
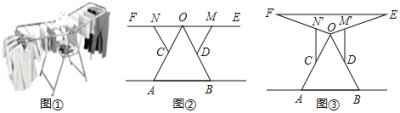
����Ŀ�������̼ҵ���̨�Ϸ�����һ�����¼ܣ���ȫ�ȹ��ſ���ͼ�٣�ͼ�ڣ��������¼ܵIJ���չ��ͼ����AOB�DZ߳�Ϊ130cm�ĵȱ������Σ����¼�OE��OF����OΪԲ��ת������OE��OF��130cm����OA��OB�ϵĵ�C��D���ֱ���֧�Ÿ�CN��DM����C��DΪԲ��ת����
��1����ͼ�ڣ���EFƽ���ڵ���AB�������̵��·������¼��ϵ��ܳ�����110cm�����������¸�OE���Ƿ���ϵ������ϣ�˵�����ɣ�
��2����ͼ�ۣ���֧�Ÿ�DM֧����M������ʱ��EOB��78������E�����������֤�·����ϵ������ϣ��·������¼��ϵ��ܳ����ԼΪ�������ף������ȡ�����ο����ݣ���![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶�ס�������ֱ�ѡ5��ͬѧ�μ���ѧ��������ݽ���������Ԥ���ɼ���ͼ��

��1��������ͼ����±���ȱ���ݣ�
ƽ���� | ��λ�� | ���� | ���� | |
�װ� | 8.5 | 8.5 | ||
�Ұ� | 8 | 10 | 1.6 |
��2�������ϱ��е�ƽ��������λ���ͷ�������Ϊ�İ�ijɼ��Ϻã���˵���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
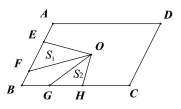
����Ŀ����O��ƽ���ı���ABCD�ĶԳ�������AD��AB��E��F�ֱ���AB���ϵĵ�����EF��![]() AB��G��H�ֱ���BC���ϵĵ�����GH��
AB��G��H�ֱ���BC���ϵĵ�����GH��![]() BC����S1,S2�ֱ��ʾEOF��GOH���������S1,S2֮��ĵ�����ϵ��______________
BC����S1,S2�ֱ��ʾEOF��GOH���������S1,S2֮��ĵ�����ϵ��______________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪������y=x2-2mx-3m
��1����m=1ʱ��
�������ߵĶԳ���Ϊֱ��______��
����������һ��P��x��ľ���Ϊ4�����P������
�۵�n��x��![]() ʱ������ֵy��ȡֵ��Χ��-
ʱ������ֵy��ȡֵ��Χ��-![]() ��y��2-n����n��ֵ
��y��2-n����n��ֵ
��2����������y=x2-2mx-3m��2m-1��x��2m+1����͵��������Ϊy0��ֱ��д��y0��m֮��ĺ�����ϵʽ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
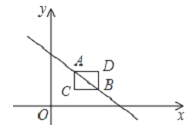
����Ŀ����ͼ������C��2��1���ֱ���x�ᡢy���ƽ���ߣ���ֱ��y=��x+4��B��A���㣬�����κ���y=ax2+bx+c��ͼ������ԭ��O���Ҷ����ھ���ADBC�ڣ��������ϣ�����a��ȡֵ��Χ��____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
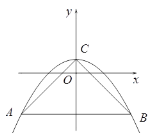
����Ŀ����ͼ��������![]() ����㣨0��-3����ƽ����x���ֱ���ཻ�ڵ�
����㣨0��-3����ƽ����x���ֱ���ཻ�ڵ�![]() ��
��![]() ����
����![]() �ύ�ڵ�C����
�ύ�ڵ�C����![]() Ϊֱ�ǣ���a=_______
Ϊֱ�ǣ���a=_______
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ�ֳɱ�Ϊÿ��![]() Ԫ�ķ�װ���涨�����ڼ����۵��۲����ڳɱ����ۣ��һ������ø��ڳɱ���
Ԫ�ķ�װ���涨�����ڼ����۵��۲����ڳɱ����ۣ��һ������ø��ڳɱ���![]() �����������֣�������
�����������֣�������![]() (��)�����۵���
(��)�����۵���![]() (Ԫ)����һ�κ���
(Ԫ)����һ�κ���![]() ���ҵ�
���ҵ�![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() .
.
(1)��![]() ��
��![]() ֮��ĺ�������ʽ.
֮��ĺ�������ʽ.
(2)�������ڼ䣬�����̳��������Ϊ![]() Ԫ��д������
Ԫ��д������![]() �����۵���
�����۵���![]() ֮��Ĺ�ϵʽ�������������
֮��Ĺ�ϵʽ�������������![]() Ԫʱ�����۵���.
Ԫʱ�����۵���.
(3)�������ڼ䣬���۵��۶�Ϊ����Ԫʱ���̳��ɻ�����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com