
����Ŀ���������֣���ͼ����֪��ABC����ADE��Ϊ���������Σ�AB��AC��AD��AE���������������η�����һ��ʹ��B��D��E��ͬһֱ���ϣ�����CE��

��1����ͼ1������ABC����ACB����ADE����AED��55������֤����BAD�ա�CAE��
��2���ڣ�1���������£����BEC�Ķ�����
�ع�̽������3����ͼ2������CAB����EAD��120����BD��4��CFΪ��BCE��BE���ϵĸߣ���ֱ��д��EF�ij��ȣ�
���𰸡���1������������2��70������3��2
��������
��1������SAS֤����BAD�ա�CAE���ɣ�
��2������ȫ�������ε����ʽ�����⼴�ɣ�
��3��ͬ����֤��BAD�ա�CAE���Ƴ�EC=BD=4���ɡ�BEC=��BAC=120�����Ƴ���FCE=30�����ɽ�����⣮
��1��֤������ͼ1�У�
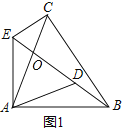
�ߡ�ABC����ACB����ADE����AED��
���EAD����CAB��
���EAC����DAB��
��AE��AD��AC��AB��
���BAD�ա�CAE��SAS����
��2���⣺��ͼ1�У���AC��BE��O��
�ߡ�ABC����ACB��55����
���BAC��180����110����70����
�ߡ�BAD�ա�CAE��
���ABO����ECO��
�ߡ�EOC����AOB��
���CEO����BAO��70����
����BEC��70����
��3���⣺��ͼ2�У�
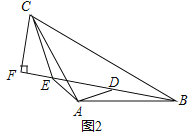
�ߡ�CAB����EAD��120����
���BAD����CAE��
��AB��AC��AD��AE��
���BAD�ա�CAE��SAS����
���BAD����ACE��BD��EC��4��
ͬ����֤��BEC����BAC��120����
���FEC��60����
��CF��EF��
���F��90����
���FCE��30����
��EF��![]() EC��2.
EC��2.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2008��5��12��14ʱ28���Ĵ��봨��������8.0��ǿ������ij�нӵ��ϼ�֪ͨ�������ɳ��ס��������������С��˳���ͬһ·�߸ϸ��������480ǧ����������������ҪЯ��һЩ�������ʣ��ȼ���ٳ���1.25Сʱ���Ӽ������ʱ��ʼ��ʱ����ͼ�е����ߡ��߶ηֱ��ʾ�ס������������·��y����ǧ�ף���y����ǧ�ף���ʱ��x��Сʱ��֮��ĺ�����ϵ��Ӧ��ͼ�������ͼ�����ṩ����Ϣ������������⣺
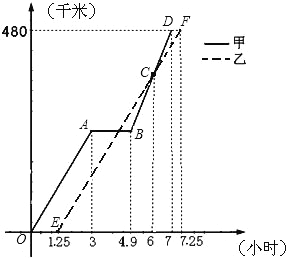
��1�����������������ϣ�������;��ͣ������ ��Сʱ��
��2������������ų����Ϻ��������ٸ������������ʼ�����������ų�����ʱ����������·���Ƕ���ǧ�ף�
��3��Ϊ�˱�֤��ʱ���磬�ס��������ڵ�һ������ʱԼ���˺�����֮���·�̲�����25ǧ�ף���ͨ������˵������ͼ������ʾ���߷��Ƿ����Լ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ԭ�ͣ���ͼ�ٵľ���MNPQ�У���E��F��G��H�ֱ���NP��PQ��QM��MN�ϣ�����1=��2=��3=��4������ı���EFGHΪ����MNPQ�ķ����ı��Σ�
������̽������ͼ�ڣ�ͼ�۵ľ���ABCD�У�AB=4��BC=8��E��F�ֱ���BC��CD���ϣ�����������������ֱ�������ͼ�о���ABCD�ķ����ı���EFGH�������ÿ�������ı���EFGH���ܳ���
������Ӧ�ã���ǰ��IJ������Է���һ�������в�ͬ�ķ����ı��Σ�����Щ�����ı��ε��ܳ�����ȣ�����ͼ�پ���MNPQ�У�MN=3��NP=4���䷴���ı���EFGH���ܳ�Ϊ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2+mx+m2=0.
(1)��֤������mȡ��ʵ�����÷��̶�����������ȵ�ʵ������
(2)���÷��̵�һ����Ϊ1����÷��̵���һ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣�ˮ�����Ű�����ÿ��2Ԫ�ļ۸�ij��ˮ�����ɽȻ����ÿ��4Ԫ�ļ۸���ۣ�ÿ����۳�100�ͨ�����鷢�֣�����ˮ��ÿ����ۼ�ÿ����0.1Ԫ��ÿ��ɶ��۳�20�Ϊ��֤ÿ�������۳�260��Ű��̾����������ۣ�
��1����������ˮ��ÿ����ۼ۽���xԪ����ÿ����������� ��ú�x�Ĵ���ʽ��ʾ����
��2����������ˮ��Ҫ��ÿ��ӯ��300Ԫ���Ű����轫ÿ����ۼ۽��Ͷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ϊ�������˿ͣ�������һ����������ת����ת�̣���ͼ��ת�̱�ƽ���ֳ�![]() �ݣ������涨���˿�ÿ������
�ݣ������涨���˿�ÿ������![]() Ԫ�����ܻ��һ��ת��ת�̵Ļ��ᣮ���ת��ֹͣ��ָ�����ö���ɫ����ɫ����ɫ������ô�˿;Ϳ��Էֱ���
Ԫ�����ܻ��һ��ת��ת�̵Ļ��ᣮ���ת��ֹͣ��ָ�����ö���ɫ����ɫ����ɫ������ô�˿;Ϳ��Էֱ���![]() Ԫ��
Ԫ��![]() Ԫ��
Ԫ��![]() Ԫ�Ĺ���ȯ��ƾ����ȯ�����ڸ��̳������������˿Ͳ�Ը��ת�̣���ô��ֱ�ӻ��
Ԫ�Ĺ���ȯ��ƾ����ȯ�����ڸ��̳������������˿Ͳ�Ը��ת�̣���ô��ֱ�ӻ��![]() Ԫ�Ĺ���ȯ��
Ԫ�Ĺ���ȯ��
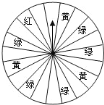
![]() ��ת��һ��ת�̻�ù���ȯ�ĸ��ʣ�
��ת��һ��ת�̻�ù���ȯ�ĸ��ʣ�
![]() תת�̺�ֱ�ӻ�ù���ȯ������Ϊ���ַ�ʽ�Թ˿����㣿
תת�̺�ֱ�ӻ�ù���ȯ������Ϊ���ַ�ʽ�Թ˿����㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
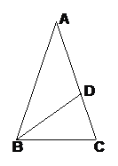
����Ŀ����ͼ����֪��ABC�У�D��AC����һ�㣬��A=36����C=72����ADB=108��
��֤��(1)AD=BD=BC��
(2)��D���߶�AC�Ļƽ�ָ�㡣
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ��ٻش����⣺��һЩ����ͼ�ο��Ա�ij��ֱ�߷ֳ������ȵ������֣����ǽ�����һ������ͼ�ηֳ������ȵ������ֵ�ֱ�߽�����ͼ�εĶ����ߡ����磺Բ��ֱ�����ڵ�ֱ����Բ�ġ������ߡ��������εĶԽ������ڵ�ֱ���������εġ������ߡ���
����������⣺
��1�����εġ������ߡ�������____________________________________��
��2�������εġ������ߡ�������__________________________________��
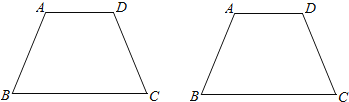
��3������ͼ�У��������ֲ�ͬ�ķ����ֱ���������ABCD�ġ������ߡ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й���![]() �Ķ�������ʽ�У�
�Ķ�������ʽ�У�![]() ��ʾʵ��������ʵ����Χ��һ���ֽܷ���ʽ���ǣ� ��
��ʾʵ��������ʵ����Χ��һ���ֽܷ���ʽ���ǣ� ��
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com