
【题目】如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化的过程中,有下列结论:
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为 ![]() .
.
其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】连接CD,∵∠C=90°,AC=BC=4,∵△ABC是等腰直角三角形,∴∠A=∠B=45°,
∵D为AB的中点,∴CD⊥AB,CD=AD=BD,∴∠DCB=∠B=45°,∴∠A=∠DCF,
在△ADE和△CDF中,AE=CF,∠A=∠DCF,AD=CD ∴△ADE≌△CDF(SAS), ∴ED=DF,∠CDF=∠ADE,
∵∠ADE+∠EDC=90°, ∴∠EDC+∠CDF=90°,即∠EDF=90°, ∴△DFE是等腰直角三角形,所以①正确;
当E、F分别为AC、BC中点时,如图2,则AE=CE=CF=BF,DE=AE=CE, ∴CE=CF=DE=DF,
而∠ECF=90°, ∴四边形CDFE是正方形,所以②错误;
∵△ADE≌△CDF, ∴S△ADE=S△CDF,
∴S四边形CEDF=S△CDE+S△CDF=S△CDE+S△ADE=S△ADC= ![]() S△ABC=
S△ABC= ![]() ×
× ![]() ×4×4=4,所以③错误;
×4×4=4,所以③错误;
∵△CEF和△DEF都为直角三角形, ∴点C、D在以EF为直径的圆上,即点C、E、D、F四点在同一个圆上,
∵△DEF是等腰直角三角形,∴EF= ![]() DE,当DE⊥AC时,DE最短,此时DE=
DE,当DE⊥AC时,DE最短,此时DE= ![]() AC=2,
AC=2,
∴EF的最小值为2 ![]() ,即点C到EF的最小距离为
,即点C到EF的最小距离为 ![]() ,所以④正确.
,所以④正确.
连接CD,根据等腰直角三角形的性质得∠A=∠B=45°,根据等腰三角形的三线合一得CD⊥AB,CD=AD=BD,根据等边对等角得出∠DCB=∠B=45°,∴∠A=∠DCF,从而利用SAS判断出△ADE≌△CDF,根据全等三角形对应边,对应角相等得出ED=DF,∠CDF=∠ADE,根据等量代换得出∠EDF=90°,故△DFE是等腰直角三角形;当E、F分别为AC、BC中点时,如图2,则AE=CE=CF=BF,DE=AE=CE, 故CE=CF=DE=DF,
而∠ECF=90°, 从而知四边形CDFE是正方形;根据全等三角形的面积相等得出S△ADE=S△CDF,然后由S四边形CEDF=S△CDE+S△CDF=S△CDE+S△ADE=S△ADC= ![]() S△ABC;根据圆周角定理判断出点C、D在以EF为直径的圆上,即点C、E、D、F四点在同一个圆上,又△DEF是等腰直角三角形,根据勾股定理得出EF=
S△ABC;根据圆周角定理判断出点C、D在以EF为直径的圆上,即点C、E、D、F四点在同一个圆上,又△DEF是等腰直角三角形,根据勾股定理得出EF=![]() DE,当DE⊥AC时,DE最短,此时DE=
DE,当DE⊥AC时,DE最短,此时DE= ![]() AC=2,从而求出EF的最小值。
AC=2,从而求出EF的最小值。


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E.下列结论错误的是( )
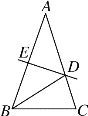
A. BD平分∠ABC B. △BCD的周长等于AB+BC
C. AD=BD=BC D. 点D是线段AC的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
A.![]()
B.![]()
C.4
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
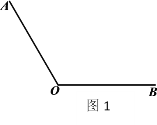
【题目】下面是小明设计的“作角的平分线”的尺规作图的过程.
已知:如图1,![]() .
.
求作:射线![]() ,使它平分
,使它平分![]() .
.
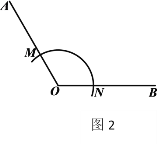
作法:如图2,
①以点![]() 为圆心,任意长为半径作弧,交
为圆心,任意长为半径作弧,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ;
;
②分别以点![]() ,
,![]() 为圆心,以大于
为圆心,以大于![]() 的同样长为半径作弧,两弧交于点
的同样长为半径作弧,两弧交于点![]() ;
;
③作射线![]() .
.
所以射线![]() 就是所求作的射线.
就是所求作的射线.
根据小明设计的尺规作图的过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,
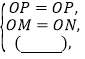
∴![]() ≌
≌![]() ( )(填推理的依据).
( )(填推理的依据).
∴ (全等三角形的 相等).
即射线![]() 平分
平分![]() (角平分线定义).
(角平分线定义).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个密闭不透明的盒子里有若干个白球,在不允许将球倒出来数的情况下,为估计白球数,小刚向其中放入8个黑球摇匀后,从中随意摸出一个球记下颜色,再把它放回盒中,不断重复这一过程,共摸球100次,其中20次摸到黑球,你估计盒中大约有白球( )
A.20个
B.28个
C.36个
D.32个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,D为△ABC所在平面内的一点,过D作DE∥AB,DF∥AC分别交直线AC,直线AB于点E,F.
(1)如图1,当点D在线段BC上时,通过观察分析线段DE、DF、AB之间的数量关系,并说明理由;
(2)如图2,当点D在直线BC上,其他条件不变时,试猜想线段DE、DF、AB之间的数量关系(请直接写出等式,不需证明);
(3)如图3,当点D是△ABC内一点,过D作DE∥AB,DF∥AC分别交直线AC,直线AB和直线BC于E、F和G. 试猜想线段DE、DF、DG与AB之间的数量关系(请直接写出等式,不需证明).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com