
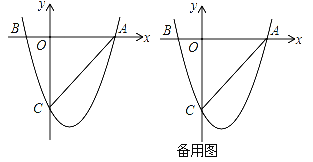
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0����ͼ����x�ύ��A��3��0����B����1��0����������y���ཻ�ڵ�C��0����3��
��1����ö��κ����Ľ���ʽ��
��2����E��y���Ҳ������������ڵ�A��һ������������E��x���ƽ���߽�����������һ��F������F��FG��ֱ��x���ڵ�G���ٹ���E��EH��ֱ��x���ڵ�H���õ�����EFGH�����ڵ�E���˶���������������EFGHΪ������ʱ������������εı߳���
��3����P����x���·����������ϵ�һ������������PA��PC������PAC�����ȡֵ��Χ������PAC���Ϊ����ʱ����������PAC�м�����
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ����5����
����5����
�������������������1���轻��ʽΪy=a��x+1����x-3����Ȼ���C������������a���ɣ�
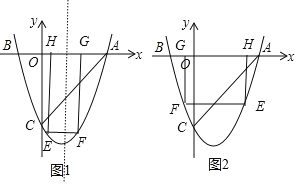
��2����E��t��t2-2t-3�������ۣ���0<t<1ʱ����ͼ1��EF=2��1-t����EH=-��t2-2t-3�������������ε����ʵ�2��1-t��=-��t2-2t-3������1<t<3ʱ����ͼ2�����������ε����ʵ�2��t-1��=-��t2-2t-3������t>3ʱ��2��t-1��=t2-2t-3��Ȼ��ֱ�ⷽ�̵õ�����������t��ֵ���ټ������Ӧ�������εı߳���
��3����P��x��x2-2x-3�������ۣ���-1<x<0ʱ������S��ABC=6����0<S��APC<6����0<x<3ʱ����PM��y�ύAC�ڵ�M����ͼ3�����ֱ��AC�Ľ���ʽΪy=x-3����M��x��x-3�������������������ʽ��S��APC=![]() 3��-x2+3x�������ö��κ��������ʵ�0<S��APC<
3��-x2+3x�������ö��κ��������ʵ�0<S��APC<![]() ������0<S��APC<6�����ǵõ���PAC���Ϊ����ʱ������ֵΪ1��2��3��4��5��
������0<S��APC<6�����ǵõ���PAC���Ϊ����ʱ������ֵΪ1��2��3��4��5��
���������(1)�������߽���ʽΪy=a(x+1)(x3)��
��C(0,3)�����3a=3�����a=1��
���������߽���ʽΪy=(x+1)(x3)��
��y=x22x3��
(2)�����ߵĶԳ���Ϊֱ��x=1��
��E(t,t22t3)��
��0<t<1ʱ,��ͼ1,EF=2(1t),EH=(t22t3)��
�߾���EFGHΪ�����Σ�
��EF=EH,��2(1t)=(t22t3)��
������t24t1=0,���t1=2+![]() (��ȥ),t2=2
(��ȥ),t2=2![]() (��ȥ)��
(��ȥ)��
��1<t<3ʱ,��ͼ2,EF=2(t1),EH=(t22t3)��
�߾���EFGHΪ�����Σ�
��EF=EH,��2(t1)=(t22t3)��
������t25=0,���t1=![]() ,t2=
,t2=![]() (��ȥ)��
(��ȥ)��
��ʱ������EFGH�ı߳�Ϊ2![]() 2��
2��
��t>3ʱ,EF=2(t1),EH=t22t3,
�߾���EFGHΪ�����Σ�
��EF=EH,��2(t1)=t22t3��
������t24t1=0,���t1=2+![]() ,t2=2
,t2=2![]() (��ȥ)��
(��ȥ)��
��ʱ������EFGH�ı߳�Ϊ2![]() +2��
+2��
��������,������EFGH�ı߳�Ϊ2![]() 2��2
2��2![]() +2��
+2��
(3)��P(x,x22x3)��
��1<x<0ʱ��
��S��ABC=![]() ��4��3=6��
��4��3=6��
��0<S��APC<6��
��0<x<3ʱ,��PM��y�ύAC�ڵ�M����ͼ3��
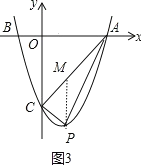
��ֱ��AC�Ľ���ʽΪy=x3,��M(x,x3)��
��PM=x3(x22x3)=x2+3x��
��S��APC=![]() ��3(x2+3x)=
��3(x2+3x)=![]() x2+
x2+![]() x=
x=![]() (x
(x![]() )2+
)2+![]() ��
��
��x=![]() ʱ,S��APC����������ֵΪ
ʱ,S��APC����������ֵΪ![]() ,��0<S��APC<
,��0<S��APC<![]() ��
��
��������,0<S��APC<6��
���PAC���Ϊ����ʱ������ֵΪ1��2��3��4��5������PAC��5��.


 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д� ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽�����ɣ������п���ֱ��Ӧ�õĽ��ۣ�������ֱ��ƽ�У���ô��һ��ֱ������ȡһ�㣬���������ֱ�ߵ�ʲôλ�ã���㵽��һ��ֱ�ߵľ�������.���磺��ͼ1����ֱ��![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() .
.
��ͼ2����ֱ֪��![]() ��
��![]() ��
��![]() ��
��![]() Ϊֱ��
Ϊֱ��![]() �ϵ����㣬
�ϵ����㣬![]() .
.![]() Ϊֱ��
Ϊֱ��![]() �ϵ�����.
�ϵ�����.
��1����д��ͼ�������ȵĸ��������Σ� .
��2�����![]() ��
��![]() ��
��![]() Ϊ�������㣬��
Ϊ�������㣬��![]() ��
��![]() ���ƶ�����ô����
���ƶ�����ô����![]() ���ƶ����κ�λ�������У� ��
���ƶ����κ�λ�������У� ��![]() �������ȣ������ǣ� .
�������ȣ������ǣ� .

������⣺
��ͼ3�������![]() ���Ŵ�үʮ��ǰ�а���һ�����ص�ʾ��ͼ���������꿪�ѻĵأ����ѱ����ͼ4��ʾ����״�����а������뿪�ѻĵصķֽ�С·��ͼ4������
���Ŵ�үʮ��ǰ�а���һ�����ص�ʾ��ͼ���������꿪�ѻĵأ����ѱ����ͼ4��ʾ����״�����а������뿪�ѻĵصķֽ�С·��ͼ4������![]() ���������ţ��Ŵ�ү�����
���������ţ��Ŵ�ү�����![]() ��һ��ֱ·��ֱ·�ú�Ҫ����ֱ·��ߵ����������а�ʱ��һ����.���������ϵļ���֪ʶ�����Ŵ�ү��Ҫ����Ƴ���·����.�����Ʒֽ�С·��ֱ·��ռ�������
��һ��ֱ·��ֱ·�ú�Ҫ����ֱ·��ߵ����������а�ʱ��һ����.���������ϵļ���֪ʶ�����Ŵ�ү��Ҫ����Ƴ���·����.�����Ʒֽ�С·��ֱ·��ռ�������
��1��д����Ʒ���������ͼ4�л�����Ӧ��ͼ�Σ�
��2��˵�������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
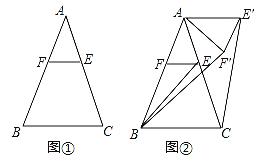
����Ŀ����֪����ABC����AB=AC����E�DZ�AC��һ��������E��EF��BC��AB�ڵ�F
��1����ͼ�٣���֤��AE=AF��
��2����ͼ�ڣ�����AEF�Ƶ�A��ʱ����ת����0�㣼����144�㣩�õ���AE��F��������CE��BF�䣮
����BF��=6����CE���ij���
������EBC=��BAC=36�㣬��ͼ������ת����������CE���ABʱ��ֱ��д����ת�����Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Դ�����������ܣ�Խ��Խ�ܵ������ߵ�ϲ��.����Ʒ�����Ͷ���г�.һ��ó��˾����ijƷ������Դ����.ȥ�������ܶ�Ϊ5000��Ԫ������1~5�·ݣ�ÿ���������ۼ۸��ȥ�꽵��1��Ԫ.����������ȥ��һ�������ͬ.�����ܶ��ȥ��һ�������20%������1~5�·�ÿ���������ۼ۸��Ƕ�����Ԫ?�����1~5�·�ÿ���������ۼ۸�Ϊx��Ԫ.�������⣬�з�����ȷ����( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
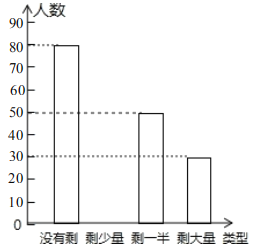
����Ŀ��Ϊ���õؼ������������ļ�ֵ�ۣ���ͬѧ����ϧ��ʳ��ѧ��ж���Уѧ�����������������С�ж�����ij����ͺ�ѧ����ɲ���������˲���ͬѧ�Ͳͷ��˵�ʣ��������������ͳ�ƺ���Ƴ�����ͼ��ʾ�IJ�������ͳ��ͼ.
(1)��α������ͬѧ���� ����
(2)��ȫ����ͳ��ͼ��
(3)����������ͳ��ͼ��ʣ������������Ӧ����Բ�ĵĶ�����
(4)Уѧ����ͨ�����ݷ�����������α����������ѧ��һ���˷ѵ�ʳ����Թ�50����һ�ͣ��ݴ˹��㣬ȫУ![]() ��ѧ��һ���˷ѵ�ʳ��ɹ�������ʳ��һ�ͣ�
��ѧ��һ���˷ѵ�ʳ��ɹ�������ʳ��һ�ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
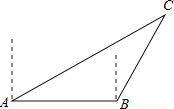
����Ŀ��������һ����C��������Χ12�����а������洬������Ⱥ��������![]() ��A����õ���C�ڱ�ƫ��60�㣬����20�����B�㣬��ʱ��õ���C�ڱ�ƫ��30�㣬����洬���ı亽�������У���û�д�����Σ�գ�
��A����õ���C�ڱ�ƫ��60�㣬����20�����B�㣬��ʱ��õ���C�ڱ�ƫ��30�㣬����洬���ı亽�������У���û�д�����Σ�գ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʡ���ҹ����������ۺ������������������ƶ����÷�չ�����ƹ�������ȷ���������ʾ����ļ�ֵ��Ϊ����������Ӧ��ʾ�����У�����ij���������������ĵ�����������Ϣ������������飨��������ÿ����ѡһ��������Dz�������������Ϣ��ע��ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣺

��1�����β������������� �ˣ�
��2����ע����ҽ����Ϣ���� �ˣ�����ȫ����ͳ��ͼ��
��3������ͳ��ͼ�У�D���ֵ�Բ�Ľ��� �ȣ�
��4��˵һ�����ͳ��ͼ�л�ȡ����Ϣ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�����ӵij���Ϊ25�ף�б����ǽ�ϣ����ӵͲ���ǽ��Ϊ7�ף�
��1��������Ӷ������������ ���ף�
��2��������ӵĶ����»���4�ף���ô���ӵĵײ���ˮƽ�����˼��ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й������е�һ������2,4,6,8,10,12����������ÿһ�����ʽ��2n(n��������)����ʾ����ô�й������е�һ��������1,2����4,7����11,16����22,29����.
(1)���ĵ�10�����Ƕ�����
(2)����Ϊ���ĵ�n�����������ʽ������ʾ��
(3)2018�Dz����������е�������������ǵڼ������������������˵��������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com