
【题目】某部门为新的生产线研发了一款机器人,为了了解它的操作技能情况,在相同条件下与人工操作进行了抽样对比.过程如下,请补充完整.
收集数据对同一个生产动作,机器人和人工各操作20次,测试成绩(十分制)如下:
机器人 | 8.0 | 8.1 | 8.1 | 8.1 | 8.2 | 8.2 | 8.3 | 8.4 | 8.4 | 9.0 |
9.0 | 9.0 | 9.1 | 9.1 | 9.4 | 9.5 | 9.5 | 9.5 | 9.5 | 9.6 | |
人工 | 6.1 | 6.2 | 6.6 | 7.2 | 7.2 | 7.5 | 8.0 | 8.2 | 8.3 | 8.5 |
9.1 | 9.6 | 9.8 | 9.9 | 9.9 | 9.9 | 10 | 10 | 10 | 10 |
整理、描述数据按如下分段整理、描述这两组样本数据:
成绩x 人数 生产方式 | 6≤x<7 | 7≤x<8 | 8≤x<9 | 9≤x≤10 |
机器人 | 0 | 0 | 9 | 11 |
人工 |
|
|
|
(说明:成绩在9.0分及以上为操作技能优秀,8.0~8.9分为操作技能良好,6.0~7.9分为操作技能合格,6.0分以下为操作技能不合格)
分析数据两组样本数据的平均数、中位数、众数和方差如下表所示:
平均数 | 中位数 | 众数 | 方差 | |
机器人 | 8.8 | 9.0 | 9.5 | 0.333 |
人工 | 8.6 | 8.8 | 10 | 1.868 |
得出结论
(1)如果生产出一个产品,需要完成同样的操作200次,估计机器人生产这个产品达到操作技能优秀的次数为 ;
(2)请结合数据分析机器人和人工在操作技能方面各自的优势: .
【答案】补全表格见解析;(1)110;(2)机器人的样本数据的平均数和中位数都明显高于人工,方差较小,可以推断其优势在于操作技能水平较高的同时还能保持稳定.人工的样本数据的众数为10,机器人的样本数据的最大值为9.6,可以推断人工的优势在于能完成一些最高水平的操作.
【解析】
(1)根据题目中给出的数据,补全数据表格,找出机器人成绩在9.0以上的人数占操作次数的比例,然后与总次数200相乘即可解决.
(2)根据样本数据中平均数、中位数判断判断机器人和人工的技能水平,通过方差数据判断两者的稳定性,通过众数推断人工和机器人在高水平操作上的优劣势.
解:补全表格如下:
6≤x<7 | 7≤x<8 | 8≤x<9 | 9≤x≤10 | |
机器人 | 0 | 0 | 9 | 11 |
人工 | 3 | 3 | 4 | 10 |
平均数 | 中位数 | 众数 | 方差 | |
机器人 | 8.8 | 9.0 | 9.5 | 0.333 |
人工 | 8.6 | 8.8 | 10 | 1.868 |
(1)![]() 200=110;
200=110;
(2)机器人的样本数据的平均数和中位数都明显高于人工,方差较小,可以推断其优势在于操作技能水平较高的同时还能保持稳定.人工的样本数据的众数为10,机器人的样本数据的最大值为9.6,可以推断人工的优势在于能完成一些最高水平的操作.


科目:初中数学 来源: 题型:
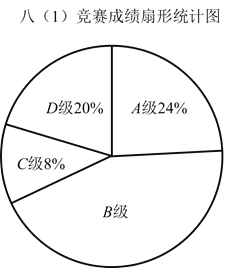
【题目】在学校组织的数学竞赛中,八(1)班比赛成绩分为![]() 、
、![]() 、
、![]() 、
、![]() 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将八(1)班成绩现整理并绘制成如下的统计图.请你根据以上提供的信息解答下列问题:
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将八(1)班成绩现整理并绘制成如下的统计图.请你根据以上提供的信息解答下列问题:
(1)请补全条形统计图
(2)八年级一班竞赛成绩众数是________,中位数落在________类.
(3)若该校有1500名学生,请估计该校本次竞赛成绩为![]() 类的学生人数.
类的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
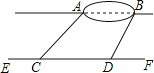
【题目】小明想测量湿地公园内某池塘两端A,B两点间的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=40°,再向前行走100米到点D处,测得∠BDF=52.44°,若直线AB与EF之间的距离为60米,求A,B两点的距离(结果精确到0.1)(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin52.44°≈0.79,cos52.44°≈0.61,tan52.44°≈1.30)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线上一点作这条直线的垂线”的尺规作图过程.
已知:直线l及直线l上一点P.
![]()
求作:直线PQ,使得PQ⊥l.
作法:如图,
![]()
①在直线l上取一点A(不与点P重合),分别以点P,A为圆心,AP长为半径画弧,两弧在直线l的上方相交于点B;
②作射线AB,以点B为圆心,AP长为半径画弧,交AB的延长线于点Q;
③作直线PQ.
所以直线PQ就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接BP,
∵ = = =AP,
∴点A,P,Q在以点B为圆心,AP长为半径的圆上.
∴∠APQ=90°( ).(填写推理的依据)
即PQ⊥l.
查看答案和解析>>
科目:初中数学 来源: 题型:
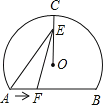
【题目】如图,点C是⊙O优弧ACB上的中点,弦AB=8cm,E为OC上任意一点,动点F从点A出发,以每秒1cm的速度沿AB方向向点B匀速运动,若y=AE2﹣EF2,则y与动点F的运动时间x(0≤x≤4)秒的函数关系式为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队5名场上队员的身高(单位:cm)是:183、187、190、200、210,现用一名身高为195cm的队员换下场上身高为210 cm的队员,与换人前相比,场上队员的身高 ( )
A.平均数变大,方差变大B.平均数变小,方差变小
C.平均数变大,方差变小D.平均数变小,方差变大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解初中学生每天在校体育活动的时间(单位:![]() ),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
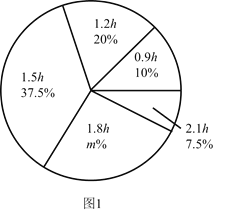
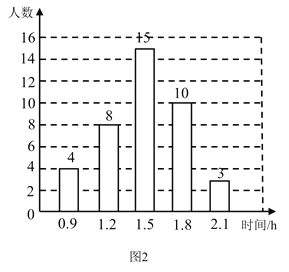
(Ⅰ)本次接受调查的初中学生人数为 ,图1中![]() 的值为 ;
的值为 ;
(Ⅱ)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有1200名初中学生,估计该校每天在校体育活动时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生对世博礼仪的知晓程度,从全校1200名学生中随机抽取了50名学生进行测试.根据测试成绩(成绩取整数,满分为100分)作了统计分析,绘制成频数分布直方图(如图,其中部分数据缺失).又知90分以上(含90分)的人数比60~70分(含60分,不含70分)的人数的2倍还多3人.请你根据上述信息,解答下列问题:
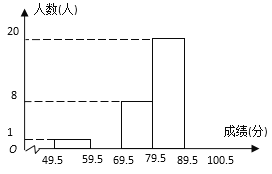
(1)该统计分析的样本是( )
A.1200名学生;
B.被抽取的50名学生;
C.被抽取的50名学生的问卷成绩;
D.50
(2)被测学生中,成绩不低于90分的有多少人?
(3)测试成绩的中位数所在的范围是 ;
(4)如果把测试成绩不低于80分记为优良,试估计该校有多少名学生对世博礼仪的知晓程度达到优良;
(5)学校准备从这50名学生中,以测试成绩不低于90分为标准,随机选3人义务宣传世博礼仪,若小杰的得分是93分,那么小杰被选上的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com