
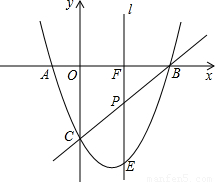
 )2+
)2+ (0≤a≤3)
(0≤a≤3) .
. ,0).
,0). .
.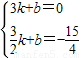 ,
,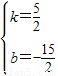 ,
, x-
x-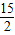 .
.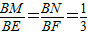
 ,
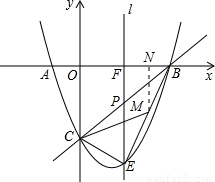
, ,0),又直线BE过M点.
,0),又直线BE过M点. ,-
,- ).
). =(
=( -1-k)2-4,
-1-k)2-4,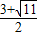 (负值舍去).
(负值舍去).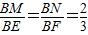
 ).
). =(2-1-k)2-4,
=(2-1-k)2-4,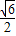 (负值舍去).
(负值舍去).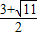 或1+
或1+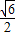 个单位长度后可得到抛物线c2.
个单位长度后可得到抛物线c2.

科目:初中数学 来源:2010年湖北省黄冈市数学中考精品试卷之四(解析版) 题型:解答题
 )
)
查看答案和解析>>
科目:初中数学 来源:2009年湖北省黄石市阳新县太子中学中考模拟数学试卷(3)(解析版) 题型:解答题
 )
)
查看答案和解析>>
科目:初中数学 来源:2009年广东省湛江市中考数学模拟试卷(解析版) 题型:解答题
 )
)
查看答案和解析>>
科目:初中数学 来源:2008年福建省莆田市中考数学试卷(网络卷)(解析版) 题型:解答题
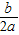 )
)
查看答案和解析>>
科目:初中数学 来源:2008年福建省莆田市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com