
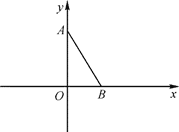
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕ xOy жаЃЌвбжЊЕу A(0ЃЌ3)ЃЌЕу B(![]() ЃЌ0)ЃЌСЌНг ABЃЎШєЖдгкЦН УцФквЛЕу CЃЌЕБЁїABC ЪЧвд AB ЮЊбќЕФЕШбќШ§НЧаЮЪБЃЌГЦЕу C ЪЧЯпЖЮ AB ЕФЁАЕШГЄЕуЁБ
ЃЌ0)ЃЌСЌНг ABЃЎШєЖдгкЦН УцФквЛЕу CЃЌЕБЁїABC ЪЧвд AB ЮЊбќЕФЕШбќШ§НЧаЮЪБЃЌГЦЕу C ЪЧЯпЖЮ AB ЕФЁАЕШГЄЕуЁБ
(1)дкЕу C1 (Ѓ2ЃЌ ![]() )ЃЌЕу C2 (0ЃЌЃ2)ЃЌЕу C3 (
)ЃЌЕу C2 (0ЃЌЃ2)ЃЌЕу C3 (![]() ЃЌ
ЃЌ ![]() )жаЃЌЯпЖЮ AB ЕФЁАЕШГЄЕуЁБЪЧЕу______________ЃЛ
)жаЃЌЯпЖЮ AB ЕФЁАЕШГЄЕуЁБЪЧЕу______________ЃЛ
(2)ШєЕу D( m ЃЌ n )ЪЧЯпЖЮ AB ЕФЁАЕШГЄЕуЁБЃЌЧвЁЯDABЃН60ЃЌЧѓ m КЭ n ЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉC1 ЃЌC3ЃЛЃЈ2ЃЉ![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉРћгУЙДЙЩЖЈРэЗжБ№ЧѓГіШ§НЧаЮЕФШ§ЬѕБпГЄЃЌХаЖЯЪЧЗёЪЧвдABЮЊбќЕФЕШбќШ§НЧаЮЃЛЃЈ2ЃЉЗжСНРрЧщПіЬжТлЃКЂйЕБЕуDдкyжсзѓВрЪБЃЌЂкЕБЕуDдкyжсгвВрЪБЃЌНсКЯЕШГЄЕуЕФЖЈвхЗжБ№ЧѓГіСНжжЧщПіmЁЂnЕФжЕМДПЩ.
ЪдЬтНтЮіЃК
НтЃК(1) C1 (Ѓ2ЃЌ3+2![]() )ЃЌAO=3ЃЌBO=
)ЃЌAO=3ЃЌBO=![]() ЃЌ
ЃЌ
зїC1DЁЭxжсНЛгкЕуDЃЌзїC1EЁЭyжсНЛгкЕуEЃЌ
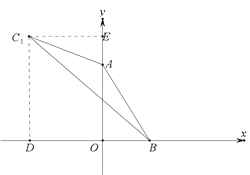
ЁрC1D=3+2![]() ЃЌC1E=2ЃЌ
ЃЌC1E=2ЃЌ
гЩЙДЙЩЖЈРэПЩЕУЃКAB=2![]() ЃЌAC1=2
ЃЌAC1=2![]() ЃЌ
ЃЌ
ЁрC1ЪЧЯпЖЮABЕФЕШГЄЕуЃЛ
ЭЌРэПЩжЄЃКC3ЪЧЯпЖЮABЕФЕШГЄЕуЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌ
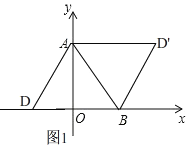
дкRtЁїAOBжаЃЌOA=3ЃЌOB=![]() ЃЌ
ЃЌ
ЁрAB=2![]() ЃЌtanЁЯOAB=
ЃЌtanЁЯOAB=![]() ЃЌ
ЃЌ
ЁрЁЯOABЃН30ЁуЃЌ
ЂйЕБЕуDдкyжсзѓВрЪБЃЌ
ЁпЁЯDABЃН60ЁуЃЌ
ЁрЁЯDAOЃНЁЯDABЃЁЯBAO= 30ЁуЃЌ
ЁпЕуD( mЃЌn )ЪЧЯпЖЮABЕФЁАЕШГЄЕуЁБЃЌ
ЁрAD=ABЃЌ
ЁрDЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
Ёрm=![]() ЃЌn=0ЃЛ
ЃЌn=0ЃЛ
ЂкЕБЕуDдкyжсгвВрЪБЃЌ
ЁпЁЯDABЃН60ЁуЃЌ
ЁрЁЯDAOЃНЁЯBAO+ЁЯDAB= 90ЁуЃЌ
Ёрn=3,
ЁпЕуD( mЃЌn )ЪЧЯпЖЮABЕФЁАЕШГЄЕуЁБЃЌ
ЁрAD=AB=2![]() ЃЌ
ЃЌ
Ёрm=2![]() .
.
Ёрm=2![]() ЃЌn=3.
ЃЌn=3.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊBЁЂCЁЂEШ§ЕудкЭЌвЛЬѕжБЯпЩЯЃЌЁїABCгыЁїDCEЖМЪЧЕШБпШ§НЧаЮ.ЦфжаЯпЖЮBDНЛACгкЕуGЃЌЯпЖЮAEНЛCDгкЕуF.
ЧѓжЄЃКЃЈ1ЃЉЁїACEЁеЁїBCDЃЛЃЈ2ЃЉЁїGFCЪЧЕШБпШ§НЧаЮ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОјЖджЕаЁгк3.5ЕФећЪ§ЕФИіЪ§ЪЧ( ).
A. 8 B. 7 C. 6 D. 5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтЪЧМйУќЬтЕФЪЧЃЈ ЃЉ
A.СНЬѕжБЯпБЛЕкШ§ЬѕжБЯпЫљНиЃЌФкДэНЧЯрЕШ
B.дкЭЌвЛЦНУцФкЃЌДЙжБгкЭЌвЛЬѕжБЯпЕФСНЬѕжБЯпЛЅЯрЦНаа
C.ВЛЯрЕШЕФНЧВЛЪЧЖдЖЅНЧЃЛ
D.ШєвЛИіНЧЕФСНБпЗжБ№гыСэвЛИіНЧЕФСНБпЦНааЃЌФЧУДетСНИіНЧЯрЕШЛђЛЅВЙ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ xOy жаЃЌЕу P 2ЃЌ 4дкЃЈ ЃЉ
A.ЕквЛЯѓЯоB.ЕкЖўЯѓЯоC.ЕкШ§ЯѓЯоD.ЕкЫФЯѓЯо
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуDЕФзјБъЪЧЃЈЉ3ЃЌ1ЃЉЃЌЕуAЕФзјБъЪЧЃЈ4ЃЌ3ЃЉЃЎ
ЃЈ1ЃЉЕуBКЭЕуCЕФзјБъЗжБ№ЪЧ______ЁЂ______ЃЎ
ЃЈ2ЃЉНЋЁїABCЦНвЦКѓЪЙЕуCгыЕуDжиКЯЃЌЕуAЁЂBгыЕуEЁЂFжиКЯЃЌЛГіЁїDEFЃЎВЂжБНгаДГіEЁЂFЕФзјБъЃЎ
ЃЈ3ЃЉШєABЩЯЕФЕуMзјБъЮЊЃЈxЃЌyЃЉЃЌдђЦНвЦКѓЕФЖдгІЕуMЁфЕФзјБъЮЊ______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCФкНггкЁбOЃЌACЪЧжБОЖЃЌBC=BAЃЌдкЁЯACBЕФФкВПзїЁЯACF=30ЁуЃЌЧвCF=CAЃЌЙ§ЕуFзїFHЁЭACгкЕуHЃЌСЌНгBFЃЎ
ЃЈ1ЃЉШєCFНЛЁбOгкЕуGЃЌЁбOЕФАыОЖЪЧ4ЃЌЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉЧыХаЖЯжБЯпBFгыЁбOЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯAЃН80ЁуЃЌЁЯBЃН40ЁуЃЌDЃЌEЗжБ№ЪЧABЃЌACЩЯЕФЕуЃЌЧвDEЁЮBCЃЌдђЁЯAEDЕФЖШЪ§ЮЊЃЈЁЁЁЁЃЉ

A. 40Ёу B. 60Ёу C. 80Ёу D. 120Ёу
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com