
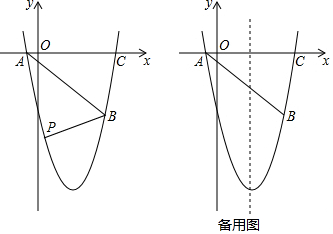
分析 (1)抛物线经过点A(-1,0),B(5,-5),C(6,0),可利用两点式法设抛物线的解析式为y=a(x+1)(x-6),代入B(5,-5)即可求得函数的解析式;
(2)作辅助线,将四边形PACB分成三个图形,两个三角形和一个梯形,设P(m,$\frac{5}{6}$m2-$\frac{25}{6}$m-5),四边形PACB的面积为S,用字母m表示出四边形PACB的面积S,发现是一个二次函数,利用顶点坐标求极值,从而求出点P的坐标.
(3)分三种情况画图:①以A为圆心,AB为半径画弧,交对称轴于Q1和Q4,有两个符合条件的Q1和Q4;②以B为圆心,以BA为半径画弧,也有两个符合条件的Q2和Q5;③作AB的垂直平分线交对称轴于一点Q3,有一个符合条件的Q3;最后利用等腰三角形的腰相等,利用勾股定理列方程求出Q3坐标.
解答 解:(1)设y=a(x+1)(x-6)(a≠0),
把B(5,-5)代入:a(5+1)(5-6)=-5,
a=$\frac{5}{6}$,
∴y=$\frac{5}{6}$(x+1)(x-6)=$\frac{5}{6}$x2-$\frac{25}{6}$x-5;
(2)存在,
如图1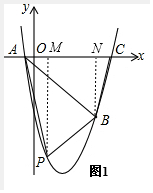 ,
,
分别过P、B向x轴作垂线PM和BN,垂足分别为M、N,
设P(m,$\frac{5}{6}$m2-$\frac{25}{6}$m-5),四边形PACB的面积为S,
则PM=-$\frac{5}{6}$m2+$\frac{25}{6}$m+5,AM=m+1,MN=5-m,CN=6-5=1,BN=5,
∴S=S△AMP+S梯形PMNB+S△BNC,
=$\frac{1}{2}$(-$\frac{5}{6}$m2+$\frac{25}{6}$m+5)(m+1)+$\frac{1}{2}$(5-$\frac{5}{6}$m2+$\frac{25}{6}$m+5)(5-m)+$\frac{1}{2}$×1×6,
=-$\frac{5}{2}$(m2-4m+4)+$\frac{81}{2}$
=-$\frac{5}{2}$(m-2)2+$\frac{81}{2}$,
当m=2时,S有最大值为$\frac{81}{2}$,这时$\frac{5}{6}$m2-$\frac{25}{6}$m-5=$\frac{5}{6}$×22-$\frac{25}{6}$×2-5=-10,
∴P(2,-10),
(3)这样的Q点一共有5个,
①以A为圆心,以AB为半径画弧,交抛物线的对称轴于Q1、Q4,则AQ1=AQ4=AB,
设对称轴交x轴于E,
y=$\frac{5}{6}$x2-$\frac{25}{6}$x-5=$\frac{5}{6}$(x-$\frac{5}{2}$)2-$\frac{245}{24}$;
∴抛物线的对称轴是:x=$\frac{5}{2}$,
∵A(-1,0),B(5,-5),
∴AB=$\sqrt{(5+1)^{2}+(-5-0)^{2}}$=$\sqrt{61}$,
∴AE=$\frac{5}{2}$+1=$\frac{7}{2}$,
由勾股定理得:Q1E=Q4E=$\sqrt{(\sqrt{61})^{2}-(\frac{7}{2})^{2}}$=$\frac{\sqrt{195}}{2}$,
∴Q1($\frac{5}{2}$,$\frac{\sqrt{195}}{2}$),Q4($\frac{5}{2}$,-$\frac{\sqrt{195}}{2}$)
②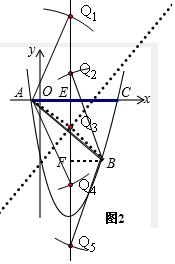 以B为圆心,以AB为半径画弧,交抛物线的对称轴于Q2、Q5,
以B为圆心,以AB为半径画弧,交抛物线的对称轴于Q2、Q5,
∴Q2F=Q5F=AB=$\sqrt{61}$,
过B作BF⊥Q1Q5于F,则Q2F=Q5F,
∵B(5,-5),
∴BF=$\frac{5}{2}$,
由勾股定理得:Q2F=$\sqrt{(\sqrt{61})^{2}-(\frac{5}{2})^{2}}$=$\frac{\sqrt{219}}{2}$,
∴Q5E=$\frac{\sqrt{219}}{2}$+5=$\frac{\sqrt{219}+10}{2}$,
∴Q5($\frac{5}{2}$,-$\frac{\sqrt{219}+10}{2}$),
∵Q2E=$\frac{\sqrt{219}}{2}$-5=$\frac{\sqrt{219}-10}{2}$,
∴Q2($\frac{5}{2}$,$\frac{\sqrt{219}-10}{2}$),
③连接Q3A、Q3B,
因为Q3在对称轴上,所以设Q3($\frac{5}{2}$,y),
∵△Q3AB是等腰三角形,且Q3A=Q3B,
由勾股定理得:($\frac{5}{2}$+1)2+y2=($\frac{5}{2}$-5)2+(y+5)2,
y=-$\frac{19}{10}$,
∴Q3($\frac{5}{2}$,-$\frac{19}{10}$).
综上所述,点Q的坐标为:Q1($\frac{5}{2}$,$\frac{\sqrt{195}}{2}$),Q2($\frac{5}{2}$,$\frac{\sqrt{219}-10}{2}$),Q3($\frac{5}{2}$,-$\frac{19}{10}$).Q4($\frac{5}{2}$,-$\frac{\sqrt{195}}{2}$)Q5($\frac{5}{2}$,-$\frac{\sqrt{219}+10}{2}$).
点评 本题考查了二次函数综合题,解(1)的关键是利用待定系数法求解析式,解(2)的关键是利用多边形的面积得出二次函数,解(3)的关键是利用等腰三角形的一些性质,注意由一个动点与两个定点组成的等腰三角形三种情况的讨论.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
 如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB于D,tan∠B=$\frac{1}{3}$,且BC=9 cm,求AC,AB及CD的长.
如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB于D,tan∠B=$\frac{1}{3}$,且BC=9 cm,求AC,AB及CD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
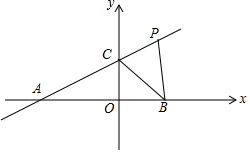 若直线y=$\frac{1}{2}$x+2分别交x轴、y轴于A、C两点,点P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,且S△ABC=6
若直线y=$\frac{1}{2}$x+2分别交x轴、y轴于A、C两点,点P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,且S△ABC=6查看答案和解析>>
科目:初中数学 来源: 题型:解答题
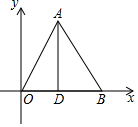 如图,△AOB是等边三角形,B点的坐标为(6,0),AD是高.
如图,△AOB是等边三角形,B点的坐标为(6,0),AD是高.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com