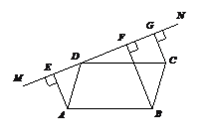
【题目】如图，直线MN过□ABCD的顶点D，过A，B，C三点，分别作MN的垂线，垂足分别是E，F，G．
求证：DE＝FG．
【答案】答案见解析
【解析】试题分析：作CH⊥BF与H．可证△AED≌△BHC，得到ED=HC，再由平行线间的距离处处相等得到FG=CH，即可得到结论．
试题解析：证明：作CH⊥BF与H．
∵AE⊥MN，BF⊥MN，∴AE∥BF，∴∠EAD+∠DAB+∠ABF=180°．
∵ABCD是平行四边形，∴AD∥BC，AD=BC，∴∠DAB+∠ABF+∠HBC=180°，∴∠EAD=∠HBC．在△AED和△BHC中，∵∠EAD=∠HBC，∠AED=∠BHC=90°，AD=BC，∴△AED≌△BHC，∴ED=HC．
∵BF⊥MN，CG⊥MN，∴BF∥CG．
∵GF⊥FB，CH⊥FB，∴FG=CH（平行线间的距离处处相等）．
∵ED=HC，∴ED=FG．
阳光课堂课时优化作业系列答案科目：初中数学 来源： 题型：
【题目】已知抛物线C：y=ax2+bx+c（a＜0）过原点，与x轴的另一个交点为B（4，0），A为抛物线C的顶点． 
（1）如图1，若∠AOB=60°，求抛物线C的解析式；
（2）如图2，若直线OA的解析式为y=x，将抛物线C绕原点O旋转180°得到抛物线C′，求抛物线C、C′的解析式；
（3）在（2）的条件下，设A′为抛物线C′的顶点，求抛物线C或C′上使得PB=PA′的点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
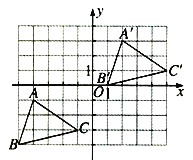
【题目】如图所示，三角形A′B′C′是三角形ABC经过平移得到的，A（-4，-1），B（-5，-4），三角形ABC中任意一点P（x1，y1）平移后的对应点为P′（x1+6，y1+4）.
（1）请写出三角形ABC平移的过程；
（2）分别写出点A′，B′，C′的坐标；
（3）求三角形A′B′C′的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列不能作为判定四边形ABCD为平行四边形的条件的是（ ）
A. AB＝CD，AD＝BC B. AB
CD
C. AB＝CD，AD∥BC D. AB∥CD，AD∥BC
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ACB＝90°，点D，E在AB上，且AF垂直平分CD，BG垂直平分CE．(1)求∠ECD的度数；(2)若∠ACB为α，则∠ECD的度数能否用含α的式子来表示．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】右图中曲线是反比例函数 
的图象的一支．
（1）这个反比例函数图象的另一支位于哪个象限？常数n的取值范围是什么？
（2）若一次函数 
的图象与反比例函数的图象交于点A，与x轴交于点B，△AOB的面积为2，求n的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
