

���� ��1����y=0�ⷽ�̼��ɣ�
��2���ô���ϵ��������������������Ľ���ʽ���ٸ���A��D��B��M����������ı���ADBM�������
��3��ͨ���ⷽ���������D���꣬����ֱ��DM��x��ļн�Ϊ45���г����̼�����⣮
��4������E��EF��y�ᣬ��ֱ��AD�ڵ�F����E��x��ax2-2ax-3a����д����ACE����ı���ʽ�����ݶ��κ��������ֵ�г����̼��ɽ����
��� �⣺��1����y=0��a��x+1����x-3��=0�����x=-1��3������A��-1��0����B��3��0����
�ʴ�ΪA��-1��0����B��3��0����
��2���߶��κ���y=a��x+1����x-3������Ϊ��1��4����
��4=-4a��
��a=-1��
��������Ϊy=-x2+2x+3
��һ�κ���y=ax+b����A��-1��0��
��0=-a+b��
��b=a��
��һ�κ���Ϊ��y=-x-1��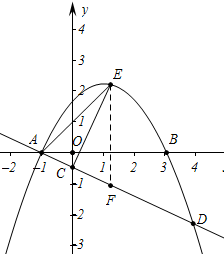
��$\left\{\begin{array}{l}{y=-x-1}\\{y={-x}^{2}+2x+3}\end{array}\right.$���$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.��\left\{\begin{array}{l}{x=4}\\{y=-5}\end{array}\right.$��
���D��4��-5����
��S�ı���ADBM=S��ABM+S��ABD=$\frac{1}{2}$��4��4+$\frac{1}{2}$��4��5=18��
��3����$\left\{\begin{array}{l}{y=ax+a}\\{y=a{x}^{2}-2ax-3a}\end{array}\right.$��õ�$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.��\left\{\begin{array}{l}{x=4}\\{y=5a}\end{array}\right.$��
���D��4��5a����
�߶���M��1��-4a����
��ֱ��DM��x��ļн�Ϊ45�㣬
��-4a-5a=4-1��
��a=-$\frac{1}{3}$��
��4������E��EF��y�ᣬ��ֱ��AD�ڵ�F����E��x��ax2-2ax-3a������F��x��ax+a����EF=ax2-2ax-3a-��ax+a��=ax2-3ax-4a��
��S��ACE=S��AFE-S��CFE=$\frac{1}{2}$��ax2-3ax-4a��•��x+1��-$\frac{1}{2}$��ax2-3ax-4a��•x=$\frac{1}{2}$��ax2-3ax-4a��=$\frac{1}{2}$a��x-$\frac{3}{2}$��2-$\frac{25}{8}a$��
�൱x=$\frac{3}{2}$ʱ����ACE������ֵ=-$\frac{25}{8}a$=$\frac{25}{4}$��
��a=-2��
���ʱ��E��$\frac{3}{2}$��$\frac{15}{2}$����
���� ���⿼����κ�����һ�κ������й����ʡ�������������ı��������֪ʶ��������ú����뷽�̵Ĺ�ϵ�ǽ������Ĺؼ�������Ƚ��ѣ���Ҫ��һ���Ĵ��������ɣ�


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��$\sqrt{2}$��$\sqrt{3}$ | B�� | 3��4��6 | C�� | $\sqrt{3}$��$\sqrt{4}$��$\sqrt{6}$ | D�� | $\sqrt{6}$��$\sqrt{8}$��$\sqrt{10}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
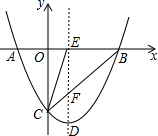 ��ͼ�����κ���y=x2+bx+c��ͼ��ֱ���x�ᡢy���ཻ��A��B��C���㣬��Գ�����x�ᡢ�߶�BC�ֱ��ڵ�E����F������CE����֪��A��-1��0����C��0��-3����
��ͼ�����κ���y=x2+bx+c��ͼ��ֱ���x�ᡢy���ཻ��A��B��C���㣬��Գ�����x�ᡢ�߶�BC�ֱ��ڵ�E����F������CE����֪��A��-1��0����C��0��-3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com