
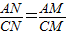 .
.
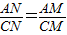 ,可以通过平行线的性质证明,需要延长AM交圆于点P,连接CP,证明PC∥BD,得出比例式,相应解决MP=CM的问题即可.
,可以通过平行线的性质证明,需要延长AM交圆于点P,连接CP,证明PC∥BD,得出比例式,相应解决MP=CM的问题即可.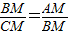 ,即BM2=AM•CM.①
,即BM2=AM•CM.①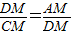 ,即DM2=AM•CM.②
,即DM2=AM•CM.②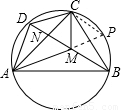
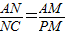 .③
.③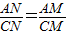 .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 BCM=∠DCN.
BCM=∠DCN.| AN |
| CN |
| AM |
| CM |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 BCM=∠DCN.
BCM=∠DCN.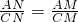 .
.查看答案和解析>>
科目:初中数学 来源:第5章《中心对称图形(二)》中考题集(57):5.7 正多边形与圆(解析版) 题型:填空题
 的中点,则△ADE的面积是 .
的中点,则△ADE的面积是 .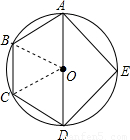
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com