
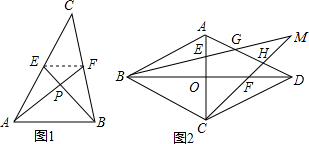
分析 (1)设PF=m,PE=n,连结EF,如图1,根据三角形中位线性质得EF∥AB,EF=$\frac{1}{2}$c,则可判断△EFP∽△BPA,利用相似比得到PB=2n,PA=2m,接着根据勾股定理得到n2+4m2=$\frac{1}{4}$b2,m2+4n2=$\frac{1}{4}$a2,则5(n2+m2)=$\frac{1}{4}$(a2+b2),而n2+m2=EF2=$\frac{1}{4}$c2,所以a2+b2=5c2;
(2)利用(1)的结论得MB2+MC2=5BC2=5×32=45,再利用△AEG∽△CEB可计算出AG=1,同理可得DH=1,则GH=1,然后利用GH∥BC,根据平行线分线段长比例定理得到MB=3GM,MC=3MH,然后等量代换后可得MG2+MH2=5.
解答 解:(1)设PF=m,PE=n,连结EF,如图1,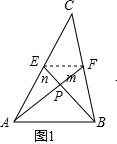
∵AF,BE是△ABC的中线,
∴EF为△ABC的中位线,AE=$\frac{1}{2}$b,BF=$\frac{1}{2}$a,
∴EF∥AB,EF=$\frac{1}{2}$c,
∴△EFP∽△BPA,
∴$\frac{EP}{BP}=\frac{PF}{PA}=\frac{EF}{BA}=\frac{1}{2}$,即$\frac{n}{PB}$=$\frac{m}{PA}$=$\frac{1}{2}$,
∴PB=2n,PA=2m,
在Rt△AEP中,∵PE2+PA2=AE2,
∴n2+4m2=$\frac{1}{4}$b2①,
在Rt△AEP中,∵PF2+PB2=BF2,
∴m2+4n2=$\frac{1}{4}$a2②,
①+②得5(n2+m2)=$\frac{1}{4}$(a2+b2),
在Rt△EFP中,∵PE2+PF2=EF2,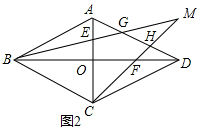
∴n2+m2=EF2=$\frac{1}{4}$c2,
∴5•$\frac{1}{4}$c2=$\frac{1}{4}$(a2+b2),
∴a2+b2=5c2;
(2)∵四边形ABCD为菱形,
∴BD⊥AC,
∵E,F分别为线段AO,DO的中点,
由(1)的结论得MB2+MC2=5BC2=5×32=45,
∵AG∥BC,
∴△AEG∽△CEB,
∴$\frac{AG}{BC}$=$\frac{AE}{CE}$=$\frac{1}{3}$,
∴AG=1,
同理可得DH=1,
∴GH=1,
∴GH∥BC,
∴$\frac{MG}{MB}$=$\frac{MH}{MC}$=$\frac{GH}{BC}$=$\frac{1}{3}$,
∴MB=3GM,MC=3MH,
∴9MG2+9MH2=45,
∴MG2+MH2=5.
点评 本题考查了相似三角形的判定:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;有两组角对应相等的两个三角形相似.也考查了三角形中位线性质和菱形的性质.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:解答题
 已知:x为实数,[x]表示不超过x的最大整数,如[3.14]=3,[1]=1,[-1.2]=-2.请你在学习,理解上述定义的基础上,解决下列问题:设函数y=x-[x].
已知:x为实数,[x]表示不超过x的最大整数,如[3.14]=3,[1]=1,[-1.2]=-2.请你在学习,理解上述定义的基础上,解决下列问题:设函数y=x-[x].查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,∠ABC,∠BCD的平分线BE,CF分别与AD相交于点E、F,BE与CF相交于点G,若AB=3,BC=5,CF=2,则BE的长为( )
如图,在?ABCD中,∠ABC,∠BCD的平分线BE,CF分别与AD相交于点E、F,BE与CF相交于点G,若AB=3,BC=5,CF=2,则BE的长为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 4$\sqrt{2}$ | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
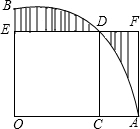 如图,扇形AOB的圆心角为直角,正方形OCDE的顶点C,E,D分别在OA,OB,弧AB上,过点A作AF⊥ED,交ED的延长线于点F,已知图中阴影部分的面积为$\sqrt{2}$-1,则正方形OCDE边长为( )
如图,扇形AOB的圆心角为直角,正方形OCDE的顶点C,E,D分别在OA,OB,弧AB上,过点A作AF⊥ED,交ED的延长线于点F,已知图中阴影部分的面积为$\sqrt{2}$-1,则正方形OCDE边长为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一条公路上依次有A、B、C三个车站,甲、乙两车同时分别从A、B车站出发,匀速开往C车站,最终到达C车站,设甲、乙两车行驶x(h)后,与B车站的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.
在一条公路上依次有A、B、C三个车站,甲、乙两车同时分别从A、B车站出发,匀速开往C车站,最终到达C车站,设甲、乙两车行驶x(h)后,与B车站的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<$\frac{9}{2}$ | B. | m<$\frac{9}{2}$且m≠$\frac{3}{2}$ | C. | m>-$\frac{9}{4}$ | D. | m>-$\frac{9}{4}$且m≠-$\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com