
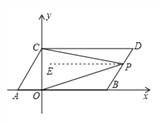
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(![]() ,0),B(
,0),B(![]() ,0),且
,0),且![]() 、
、![]() 满足
满足![]() ,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.

(1)请直接写出C,D两点的坐标.
(2)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)![]() 的值是否发生变化?并说明理由.
的值是否发生变化?并说明理由.
(3)在坐标轴上是否存在一点M,使三角形MBC的面积与三角形ACD的面积相等?若存在直接写出点M的坐标,若不存在,试说明理由.
【答案】(1)C(0,2) D(4,2)(2) ![]() ,比值不变(3)M点的坐标为(0,
,比值不变(3)M点的坐标为(0, ![]() )或(0,-
)或(0,-![]() )或(7,0)或(-1,0)
)或(7,0)或(-1,0)
【解析】分析:(1)、首先根据非负数的性质得出得出a和b的值,从而得出点A和点B的坐标,然后根据点的平移法则得出点C和点D的坐标;(2)、过点P作PE∥AB,根据平行线的性质得出∠DCP=∠CPE,∠BOP=∠OPE,从而根据角度之间的关系得出答案;(3)、根据等积法得出点M的坐标.
详解:(1)C(0,2) D(4,2)
(2) ![]() ,比值不变,理由如下:
,比值不变,理由如下:
由平移的性质可得CD∥AB, 过点P作PE∥AB,则PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE, ∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP
∴![]()
(3)M点的坐标为(0, ![]() )或(0,-
)或(0,-![]() )或(7,0)或(-1,0)
)或(7,0)或(-1,0)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.在同一平面内,两条直线的位置只有平行和垂直两种
B.两直线平行,同旁内角相等
C.过一点有且只有一条直线与已知直线平行
D.平行于同一条直线的两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图所示,已知∠1 = ∠2,∠B = ∠C,可推得AB∥CD,

理由如下:
∵∠1 = ∠2(已知),且∠1 = ∠4(_____________________),
∴∠2 = ∠4(等量代换).
∴CE∥BF(__________________________).
∴∠_____= ∠3(________________________)
又∵∠B = ∠C(已知),
∴∠3= ∠B(等量代换),
∴AB∥CD(_____________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按HUI图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2018个点的坐标为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠1,∠2+∠3=180°.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.
(1)若|x+2y﹣5|+|2x﹣y|=0,试分别求出1秒钟后A、B两点的坐标;

(2)设∠BAO的外角和∠ABO的外角的平分线相交于点P,问:点A、B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元。
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按图填空,并注明理由.
⑴完成正确的证明:如图,已知AB∥CD,求证:∠BED=∠B+∠D
证明:过E点作EF∥AB(经过直线外一点有且只有一条直线与这条直线平行)
∴∠1= ( )
∵AB∥CD(已知)
∴EF∥CD(如果两条直线与同一直线平行,那么它们也平行)
∴∠2= ( )
又∠BED=∠1+∠2
∴∠BED=∠B+∠D (等量代换).
⑵如图,在△ABC中,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:因为EF∥AD(已知)
所以∠2=∠3.( )
又因为∠1=∠2,所以∠1=∠3.(等量代换)
所以AB∥ ( )
所以∠BAC+ =180°( ).
又因为∠BAC=70°,所以∠AGD=110°.


图⑴ 图⑵
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com