
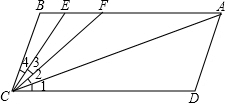
 如图,直线AB∥CD,∠B=∠D=120°,E,F在AB上,且∠1=∠2,∠3=∠4
如图,直线AB∥CD,∠B=∠D=120°,E,F在AB上,且∠1=∠2,∠3=∠4分析 (1)根据平行线的性质推出∠B+∠BCD=180°,由∠B=∠D证得∠D+∠BCD=180°,根据平行线的判定即可证得结论;
(2)根据平行线的性质推出∠B+∠BCD=180°,由∠B=∠D=120°得到∠BCD=60°,由∠1=∠2,∠3=∠4得到∠ACE=$\frac{1}{2}$(∠1+∠2+∠3+∠4)=$\frac{1}{2}$∠BCD,代入数值即可求得结论;
(3)根据平行线的性质证得∠CAF=∠1,∠CFE=∠1+∠2=2∠1,代入即可求出结论.
解答 解:(1)∵AB∥CD,
∴∠B+∠BCD=180°,
∵∠B=∠D=120°,
∴∠BCD=60°,且∠D+∠BCD=180°,
∴AD∥BC,
(2)∵∠1=∠2,∠3=∠4,
∴∠ACE=∠2+∠3=$\frac{1}{2}$(∠1+∠2)+$\frac{1}{2}$(∠3+∠4)=$\frac{1}{2}$(∠1+∠2+∠3+∠4)=$\frac{1}{2}$∠BCD=$\frac{1}{2}$×60°=30°;
(3)不变.
∵AB∥CD,
∴∠CAF=∠1,∠CFE=∠1+∠2,
∴∠CAF:∠CFE=∠1:(∠1+∠2)=∠1:2∠1=$\frac{1}{2}$,
即这两个角的比值是$\frac{1}{2}$.
点评 本题考查的是平行线的性质和判定,角平分线的定义,熟记各性质并准确识图理清图中各角度之间的关系是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:选择题
| A. | 321×102 | B. | 32.1×103 | C. | 3.21×104 | D. | 3.21×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 人数 | 2 | 3 | 4 | 1 |
| 分数 | 80 | 85 | 90 | 95 |
| A. | 90和87.5 | B. | 95和85 | C. | 90和85 | D. | 85和87.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
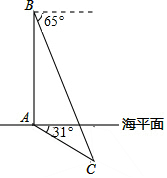 在某次反潜演习中,红方军舰A测得蓝方潜艇C的俯角为31°,位于军舰A正上方800米的红方反潜直升机B测得潜艇C的俯角为65°.试根据以上数据求出潜艇C离开海平面的下潜深度(结果保留整数)
在某次反潜演习中,红方军舰A测得蓝方潜艇C的俯角为31°,位于军舰A正上方800米的红方反潜直升机B测得潜艇C的俯角为65°.试根据以上数据求出潜艇C离开海平面的下潜深度(结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
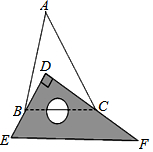 如图,将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C,若∠A=40°,求∠ABD+∠ACD=( )
如图,将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C,若∠A=40°,求∠ABD+∠ACD=( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com