
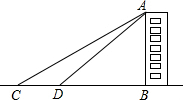
 某班开展测量教学楼高度的综合实践活动.大家完成任务的方法有很多种,其中一种方法是:如图,他们在C点测得教学楼AB的顶部点A的仰角为30°,然后向教学楼前进20米到达点D,在点D测得点A的仰角为60°,且B,C,D三点在一条直线上.请你根据这些数据,求出这幢教学楼AB的高度.
某班开展测量教学楼高度的综合实践活动.大家完成任务的方法有很多种,其中一种方法是:如图,他们在C点测得教学楼AB的顶部点A的仰角为30°,然后向教学楼前进20米到达点D,在点D测得点A的仰角为60°,且B,C,D三点在一条直线上.请你根据这些数据,求出这幢教学楼AB的高度. 科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
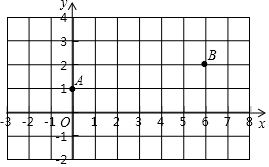 如图,在平面直角坐标系xOy中,已知点A(0,1),B(6,2),在x轴上找一点P,使得PA+PB最小,则点P的坐标是(4,0),此时△PAB的面积是2.
如图,在平面直角坐标系xOy中,已知点A(0,1),B(6,2),在x轴上找一点P,使得PA+PB最小,则点P的坐标是(4,0),此时△PAB的面积是2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
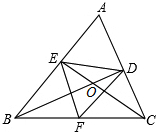 如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点O,F为BC的中点,连接EF,DF,DE,则下列结论:①EF=DF;②AD•AC=AE•AB;③△DOE∽△COB;④若∠ABC=45°时,BE=$\sqrt{2}$FC.
如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点O,F为BC的中点,连接EF,DF,DE,则下列结论:①EF=DF;②AD•AC=AE•AB;③△DOE∽△COB;④若∠ABC=45°时,BE=$\sqrt{2}$FC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com