
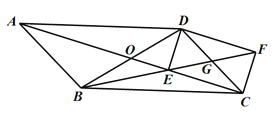
【题目】在△ABC中,∠C=90°,AC=BC,点P在线段BA的延长线上,作PD⊥AC,交AC的延长线于点D,点D关于直线AB的对称点为E,连接PE并延长PE到点F,使EF=AC,连接CF.
(1)依题意补全图1;
(2)求证:AD=CF;
(3)若AC=2,点Q在直线AB上,写出一个AQ的值,使得对于任意的点P总有QD=QF,并证明.
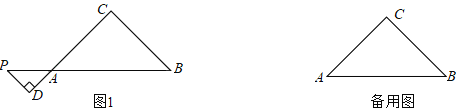
【答案】(1)见解析;(2)见解析;(3)AQ=![]() ,证明见解析.
,证明见解析.
【解析】
(1)依照题意,补全图形即可;
(2)通过证明四边形DCFP是矩形,可得PD=CF,由等腰直角三角形的性质可得AD=PD=CF;
(3)通过证明△DAQ≌△FCQ,可得QD=QF.
(1)补全图形,如图1所示:
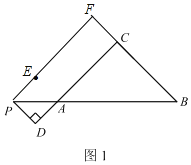
(2)∵∠C=90°,AC=BC,
∴∠B=∠CAB=45°,
∵PD⊥AC,
∴∠PDA=90°,
∴∠DPA=90°﹣∠PAD=45°=∠DAP,
∴AD=DP,
∵点D关于直线AB的对称点为E,
∴∠FPA=∠DPA=45°,PE=PD,
∴∠DPF=90°,
∴∠DPF+∠D=180°,
∴PF//CD,
又∵EF=AC,
∴EF+PE=AC+AD,
即PF=CD,
∴PF![]() CD,
CD,
∴四边形PDCF是平行四边形,
又∵∠PDA=90°,
∴四边形DCFP是矩形,
∴PD=CF,
∴AD=CF;
(3)AQ=![]() ,
,
理由如下:如图2,连接CQ,
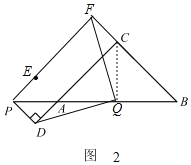
∵∠C=90°,AC=BC=2,
∴AB=2![]() ,∠B=∠CAB=45°,
,∠B=∠CAB=45°,
∵AQ=![]() ,
,
∴AQ=BQ,
又∵∠C=90°,AC=BC=2,
∴CQ=AQ=BQ,∠QCA=∠CAQ=45°,
∴∠DAQ=∠QCF=135°,
又∵AD=CF,
∴△DAQ≌△FCQ(SAS),
∴FQ=DQ.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() (
(![]() )与双曲线
)与双曲线![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() 在第一象限),直线
在第一象限),直线![]() (
(![]() )与双曲线
)与双曲线![]() 交于
交于![]() ,
,![]() 两点.当这两条直线互相垂直,且四边形
两点.当这两条直线互相垂直,且四边形![]() 的周长为
的周长为![]() 时,点
时,点![]() 的坐标为_________.
的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(﹣6,0),点B(0,8),点C在线段AB上,点D在y轴上,将∠ABO沿直线CD翻折,使点B与点A重合.若点E在线段CD延长线上,且CE=5,点M在y轴上,点N在坐标平面内,如果以点C、E、M、N为顶点的四边形是菱形,那么点N有( )
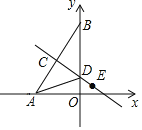
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
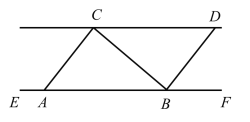
【题目】如图,为了测量某条河的对岸边C,D两点间的距离,在河的岸边与![]() 平行的直线
平行的直线![]() 上取两点A,B,测得
上取两点A,B,测得![]() ,
,![]()
![]() ,量得
,量得![]() 长为70米.求C,D两点间的距离(参考数据:
长为70米.求C,D两点间的距离(参考数据:![]() ,
,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某社区居民掌握民法知识的情况,对社区内的甲、乙两个小区各500名居民进行了测试,从中各随机抽取50名居民的成绩(百分制)进行整理、描述、分析,得到部分信息:
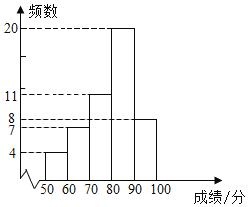
a.甲小区50名居民成绩的频数直方图如下(数据分成5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
b.图中,70≤x<80组的前5名的成绩是:79 79 79 78 77
c.图中,80≤x<90组的成绩如下:
82 | 83 | 84 | 85 | 85 | 86 | 86 | 86 | 86 | 86 |
86 | 86 | 86 | 87 | 87 | 87 | 88 | 88 | 89 | 89 |
d.两组样本数据的平均数、中位数、众数、优秀率(85分及以上)、满分人数如下表所示:
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 满分人数 |
甲 | 78.58 | 84.5 | a | b | 1 |
乙 | 76.92 | 79.5 | 90 | 40% | 4 |
根据以上信息,回答下列问题:
(1)求表中a,b的值;
(2)请估计甲小区500名居民成绩能超过平均数的人数;
(3)请尽量从多个角度,分析甲、乙两个小区参加测试的居民掌握民法知识的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图为我市某校2015年参加各类比赛(包括围棋、书法、绘画、钢琴四个类别)的参赛人数统计图:
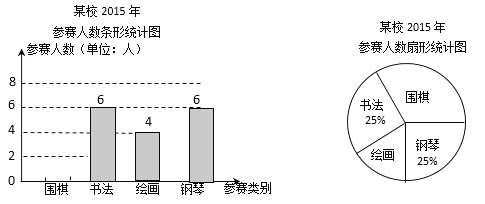
(1)该校参加比赛的总人数是 人,并把条形统计图补充完整;
(2)在扇形统计图中,该校参加围棋所对应的圆心角的度数是 ;
(3)从全市中小学参加比赛选手中随机抽取60人,其中有20人获奖.今年我市中小学参加比赛人数共有2400人,请你估算今年参加绘画比赛的人数以及参加比赛获奖的总人数约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴交于A,与y轴交于B,抛物线
与x轴交于A,与y轴交于B,抛物线![]() 经过点A,且与y轴交于点C(0,4),P为x轴上一动点,按逆时针方向作CPE,使CPE∽AOB.
经过点A,且与y轴交于点C(0,4),P为x轴上一动点,按逆时针方向作CPE,使CPE∽AOB.
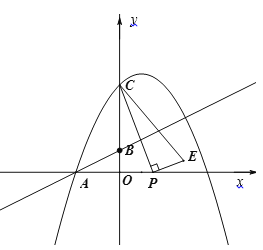
(1)求抛物线解析式.
(2)若点E落在抛物线上,求出点P的坐标.
(3)若ABE是直角三角形,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB是直线y=x+1的一部分,其中点A在y轴上,点B横坐标为2,曲线BC是双曲线![]() (
(![]() )的一部分,由点C开始不断重复“ABC”的过程,形成一组波浪线,点P(2019,m)与Q(2025,n)均在该波浪线上,G为x轴上一动点,则△PQG周长的最小值为( )
)的一部分,由点C开始不断重复“ABC”的过程,形成一组波浪线,点P(2019,m)与Q(2025,n)均在该波浪线上,G为x轴上一动点,则△PQG周长的最小值为( )

A.16B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点E为□ABCD对角线AC上的一点,点F在线段BE的延长线上,且EF=BE,线段EF与边CD相交于点G.
(1)求证:DF//AC;
(2)如果AB=BE,DG=CG,联结DE、CF,求证:四边形DECF是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com