
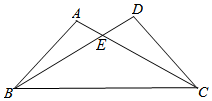
 如图,已知∠A=∠D,有下列五个条件:①AE=DE,②BE=CE,③AB=DC,④∠ABC=∠DCB,⑤AC=BD,能证明△ABC与△DCB全等的条件有几个?并选择其中一个进行证明.
如图,已知∠A=∠D,有下列五个条件:①AE=DE,②BE=CE,③AB=DC,④∠ABC=∠DCB,⑤AC=BD,能证明△ABC与△DCB全等的条件有几个?并选择其中一个进行证明. 分析 若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边;若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.
解答 解:共4个:①或②或③或④.
若选①AE=DE,理由:
在△ABE和△DCE中,
$\left\{\begin{array}{l}{∠A=∠D}\\{AE=DE}\\{∠AED=∠DEC(对顶角相等)}\end{array}\right.$,
∴AB=DC,BE=CE,
∴DE+BE=AE+CE,
∴BD=AC,
在△ABC和△DCB中,
$\left\{\begin{array}{l}{AC=BD}\\{AB=DC}\\{BC=CB}\end{array}\right.$,
∴△ABC≌△DCB(SSS);
若选②BE=CE,则证明如下:
证明:∵BE=CE
∴∠EBC=∠ECB,
在△ABC与△DCB中:
$\left\{\begin{array}{l}{∠A=∠D}\\{∠EBC=∠ECB}\\{BC=CB}\end{array}\right.$,
∴△ABC≌△DCB(AAS);
若选③AB=DC,则证明如下:
在△ABE和△DCE中,
$\left\{\begin{array}{l}{∠AEB=∠DEC}\\{∠A=∠D}\\{AB=DC}\end{array}\right.$,
∴△ABE≌△DCE(AAS),
∴BE=CE,
∴∠EBC=∠ECB,
在△ABC与△DCB中:
$\left\{\begin{array}{l}{∠A=∠D}\\{∠EBC=∠ECB}\\{BC=CB}\end{array}\right.$,
∴△ABC≌△DCB(AAS);
若选④∠ABC=∠DCB,则证明如下:
证明:在△ABC与△DCB中:
$\left\{\begin{array}{l}{∠A=∠D}\\{∠ABC=∠DCB}\\{BC=CB}\end{array}\right.$,
∴△ABC≌△DCB(AAS).
综上所述,能证明△ABC与△DCB全等的条件有4个.
点评 本题主要考查了全等三角形的判定,解题时注意:两角及其中一个角的对边对应相等的两个三角形全等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如何求tan75°的值?按下列方法作图可解决问题,如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BN上截取线段BD,使BD=AB,连接AD,依据此图可求得tan75°的值为( )
如何求tan75°的值?按下列方法作图可解决问题,如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BN上截取线段BD,使BD=AB,连接AD,依据此图可求得tan75°的值为( )| A. | 2$-\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 1+$\sqrt{3}$ | D. | $\sqrt{3}-1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,线段CD两个端点的坐标分别为C(-1,2),D(-3,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(-5,0),则点A的坐标为( )
如图,线段CD两个端点的坐标分别为C(-1,2),D(-3,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(-5,0),则点A的坐标为( )| A. | (-3,5) | B. | (-2,5) | C. | (-2,6) | D. | (-$\frac{5}{3}$,$\frac{10}{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=21m,∠BAC=53°,求这颗古杉树AB的长度.
为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=21m,∠BAC=53°,求这颗古杉树AB的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同.当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元.
某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同.当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com