
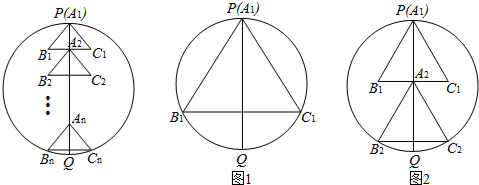
分析 设PQ与B1C1交于点D,连接B1O,得出OD=A1D-OA1,用含a1的代数式表示OD,在△OB1D中,根据勾股定理求出正三角形的边长a1;
设PQ与B2C2交于点E,连接B2O,得出OE=A1E-OA1,用含a2的代数式表示OE,在△OB2E中,根据勾股定理求出正三角形的边长a2;
设PQ与BnCn交于点F,连接BnO,得出OF=A1F-OA1,用含an的代数式表示OF,在△OBnF中,根据勾股定理求出正三角形的边长an
解答 解:(1)设PQ与B1C1交于点D,连接B1O.如图1,
∵△PB1C1是等边三角形,
∴A1D=PB1•sin∠PB1C1=a1•sin60°=$\frac{\sqrt{3}}{2}$a1,
∴OD=A1D-OA1=$\frac{\sqrt{3}}{2}$a1-1,
在△OB1D中,OB12=B1D2+OD2,
∴OD=A1D-OA1=$\frac{\sqrt{3}}{2}$a1-1,
即12=($\frac{1}{2}$a1)2+($\frac{\sqrt{3}}{2}$a1-1)2,
解得a1=$\sqrt{3}$;
(2)设PQ与B2C2交于点E,连接B2O.如图2,
∵△A2B2C2是等边三角形,
∴A2E=A2B2•sin∠A2B2C2=a2•sin60°=$\frac{\sqrt{3}}{2}$a2,
∵△PB1C1是与△A2B2C2边长相等的正三角形,
∴PA2=A2E=$\frac{\sqrt{3}}{2}$a2,
OE=A1E-OA1=$\sqrt{3}$a2-1,
在△OB2E中,OB22=B2E2+OE2,
即12=($\frac{1}{2}$a2)2+($\sqrt{3}$a2-1)2,
解得a2=$\frac{8\sqrt{3}}{13}$;
(3)设PQ与BnCn交于点F,连接BnO,
得出OF=A1F-OA1=$\frac{\sqrt{3}}{2}$nan-1,
同理,在△OBnF中,OBn2=BnF2+OF2,
即12=($\frac{1}{2}$an)2+($\frac{\sqrt{3}}{2}$nan-1)2,
解得an=$\frac{4\sqrt{3}n}{3{n}^{2}+1}$.
故答案为:$\sqrt{3}$,$\frac{{8\sqrt{3}}}{13}$,$\frac{{4\sqrt{3}n}}{{3{n^2}+1}}$.
点评 主要考查了等边三角形的性质,勾股定理等知识点.本题中a1、a2是特殊情况,注意在证明过程中抓住不变条件,从而为求a3提供思路和方法.本题综合性强,难度大,有利于培养学生分析、解决问题的能力.


科目:初中数学 来源: 题型:选择题
| A. | -2ab | B. | +2ab | C. | +4ab | D. | -4ab |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | a | C. | $\sqrt{2}$ | D. | 不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
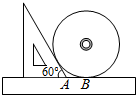 如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的半径是3$\sqrt{3}$cm.
如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的半径是3$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.求证:△PDQ是等腰直角三角形.
如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.求证:△PDQ是等腰直角三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com