
【题目】如图所示,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行____________分钟可使渔船到达离灯塔距离最近的位置.
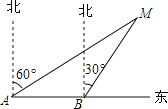
【答案】15.
【解析】
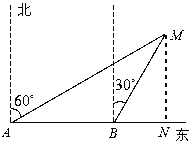
试题分析:本题主要考查了方向角含义,正确记忆三角函数的定义是解决本题的关键.需注意的是单位的统一.过M作AB的垂线,设垂足为N.由题易知∠MAB=30°,∠MBN=60°;则∠BMA=∠BAM=30°,得BM=AB.由此可在Rt△MBN中,根据BM(即AB)的长求出BN的长,进而可求出该船需要继续航行的时间.
试题解析:作MN⊥AB于N.
易知:∠MAB=30°,∠MBN=60°,
则∠BMA=∠BAM=30°.
设该船的速度为x,则BM=AB=0.5x.
Rt△BMN中,∠MBN=60°,
∴BN=12BM=0.25x.
故该船需要继续航行的时间为0.25÷x=0.25小时=15分钟.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(k1)x2+2x-2=0有不相等实数根,则k的取值范围是( )
A.k>![]() B.k≥
B.k≥![]() C.k>
C.k>![]() 且k≠1 D.k≥
且k≠1 D.k≥![]() 且k≠1
且k≠1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11分)如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
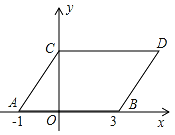
(1)求点C,D的坐标;
(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC,求出点M的坐标.
(3)若点P在直线BD上运动,连接PC,PO.
①若P在线段BD之间时(不与B,D重合),求S△CDP+S△BOP的取值范围;
②若P在直线BD上运动,请直接写出∠CPO、∠DCP、∠BOP的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明靠勤工俭学的收入维持上大学的费用,下面是小明一周的收支情况表(收入为正,单位:元)
周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
+15 | +10 | 0 | +20 | +15 | +10 | +14 |
-8 | -12 | -19 | -10 | -9 | -11 | -8 |
(1)在一周内小明有多少节余;
(2)照这样一个月(按30天计算)小明能有多少节余;
(3)按以上支出,小明一个月(按30天计算)至少要赚多少钱,才以维持正常开支.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是
A. 平行四边形的对角线互相垂直平分 B. 矩形的对角线互相垂直平分
C. 菱形的对角线互相平分且相等 D. 正方形的对角线互相垂直平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“面线”,“面线”被这个平面图形截得的线段叫做该图形的“面径”(例如圆的直径就是它的“面径”).已知等边三角形的边长为4,则它的“面径”长x的取值范围是 _.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com