
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
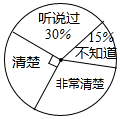 为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形统计图,若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有2700人.
为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形统计图,若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有2700人.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k<$\frac{1}{2}$且k≠0 | B. | k≤$\frac{1}{2}$且k≠0 | C. | k≥-$\frac{1}{2}$且k≠0 | D. | k>-$\frac{1}{2}$且k≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
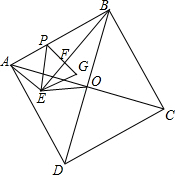 如图,正方形ABCD的边长为$\sqrt{10}$,对角线AC,BD相交于点O,以AB为斜边在正方形内部作Rt△ABE,∠ABE=90°,连接OE,点P为边AB上的一点,将△AEP沿着EP翻折到△GEP,若PG⊥BE于点F,OE=$\sqrt{2}$,则S△EPB=$\frac{3}{2}$-$\frac{3}{20}\sqrt{10}$.
如图,正方形ABCD的边长为$\sqrt{10}$,对角线AC,BD相交于点O,以AB为斜边在正方形内部作Rt△ABE,∠ABE=90°,连接OE,点P为边AB上的一点,将△AEP沿着EP翻折到△GEP,若PG⊥BE于点F,OE=$\sqrt{2}$,则S△EPB=$\frac{3}{2}$-$\frac{3}{20}\sqrt{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com