
 如图,⊙O交等边△OAB的边OA,OB于E、F,点P是⊙O上一动点,以PB为边作等边△PBD(点B、P、D顺时针排列),连接ED,若OB=10,OF=4,则ED的最小值为( )
如图,⊙O交等边△OAB的边OA,OB于E、F,点P是⊙O上一动点,以PB为边作等边△PBD(点B、P、D顺时针排列),连接ED,若OB=10,OF=4,则ED的最小值为( )| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 5 |
分析 如图,连接AD、OP.首先证明△ABD≌△OBP,推出AD=OP=4,再根据DE≥AE-AD,即可解决问题.
解答 解:如图,连接AD、OP.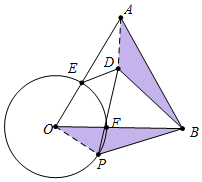
∵△OAB,△PBD都是等边三角形,OB=10,
∴BA=BO=OA=10,BD=BP,∠ABO=∠DBP=60°,
∴∠ABD=∠OBP,
在△ABD和△OBP中,
$\left\{\begin{array}{l}{BA=BO}\\{∠ABD=∠OBP}\\{BD=BP}\end{array}\right.$,
∴△ABD≌△OBP,
∴AD=OP═OF=4,
∵DE+DA≥AE,
∴DE≥AE-AD,
∵AE=OA-OE=10-4=6,AD=4,
∴DE≥2,
∴DE的最小值为2.
故选C.
点评 本题考查全等三角形的判定和性质、等边三角形的性质、两点之间线段最短等知识,解题的关键是灵活运用所学知识解决问题,学会正确寻找全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
| 用水量 | 单价(元/吨) |
| 不超过40吨的部分 | 1.8 |
| 超过40吨的部分 | 2.2 |
| 另:每吨用水加收0.2元的城市污水处理费 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 用水量 | 单价(元/吨) |
| 不超过40吨的部分 | 1.8 |
| 超过40吨的部分 | 2.2 |
| 另:每吨用水加收0.2元的城市污水处理费 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小聪做作业时不小心将墨水滴在一道数学题上,题目变为:“已知二次函数y=x2□x□的图象如图所示”,则题目中二次函数的表达式为( )
小聪做作业时不小心将墨水滴在一道数学题上,题目变为:“已知二次函数y=x2□x□的图象如图所示”,则题目中二次函数的表达式为( )| A. | y=x2+$\frac{7}{3}$x-2 | B. | y=x2-$\frac{7}{3}$x-2 | C. | y=x2+$\frac{7}{3}$x+2 | D. | y=x2-$\frac{7}{3}$x+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com