
【题目】综合与探究
如图1,平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,
,![]() .双曲线
.双曲线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
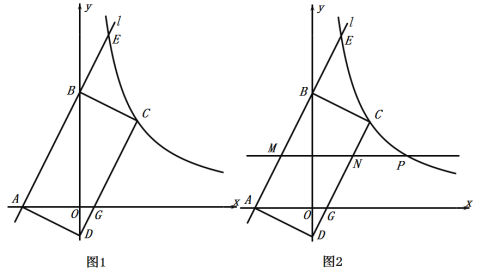
(1)求![]() 的值;
的值;
(2)在图1中以线段![]() 为边作矩形
为边作矩形![]() ,使顶点
,使顶点![]() 在第一象限、顶点
在第一象限、顶点![]() 在
在![]() 轴负半轴上.线段
轴负半轴上.线段![]() 交
交![]() 轴于点
轴于点![]() .直接写出点
.直接写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(3)如图2,在(2)题的条件下,已知点![]() 是双曲线
是双曲线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的平行线分别交线段
轴的平行线分别交线段![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
请从下列![]() ,
,![]() 两组题中任选一组题作答.我选择组题.
两组题中任选一组题作答.我选择组题.
A.①当四边形![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②在①的条件下,连接![]() ,
,![]() .坐标平面内是否存在点
.坐标平面内是否存在点![]() (不与点
(不与点![]() 重合),使以
重合),使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,直接写出点
全等?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
B.①当四边形![]() 成为菱形时,求点
成为菱形时,求点![]() 的坐标;
的坐标;
②在①的条件下,连接![]() ,
,![]() .坐标平面内是否存在点
.坐标平面内是否存在点![]() (不与点
(不与点![]() 重合),使以
重合),使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,直接写出点
全等?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ,
,![]() ;(3)A.①
;(3)A.①![]() ,②
,②![]() ,
,![]()
![]() ,
,![]() ;B.①
;B.①![]() ,②
,②![]() ,
,![]() ,
,![]() .
.
【解析】
(1)根据点![]() 在
在![]() 的图象上,求得
的图象上,求得![]() 的值,从而求得
的值,从而求得![]() 的值;
的值;
(2)点![]() 在直线
在直线![]() 上易求得点
上易求得点![]() 的坐标,证得
的坐标,证得![]() 可求得点
可求得点![]() 的坐标,证得
的坐标,证得![]() 即可求得点
即可求得点![]() 的坐标;
的坐标;
(3)A.①作![]() 轴,利用平行四边的面积公式先求得点
轴,利用平行四边的面积公式先求得点![]() 的纵坐标,从而求得答案;
的纵坐标,从而求得答案;
②分类讨论,画出相关图形,构造全等三角形结合轴对称的概念即可求解;
B.①作![]() 轴,根据菱形的性质结合相似三角形的性质先求得点
轴,根据菱形的性质结合相似三角形的性质先求得点![]() 的纵坐标,从而求得答案;
的纵坐标,从而求得答案;
②分类讨论,画出相关图形,构造全等三角形结合轴对称的概念即可求解;
(1)![]() 在
在![]() 的图象上,
的图象上,
![]() ,
,
![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,
,
![]() 在
在![]() 的图象上,
的图象上,
∴![]() ,
,
∴![]() ;
;
(2)对于一次函数![]() ,
,
当![]() 时,
时,![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,
,
当![]() 时,
时,![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,
,
∴![]() ,
,![]() ,
,
在矩形![]() 中,
中,
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,
,
矩形ABCD中,AB∥DG,
∴![]()
![]()
![]()
![]()
∴点![]() 的坐标是
的坐标是![]() ,
,
故点![]() ,
,![]() ,
,![]() 的坐标分别是:
的坐标分别是:![]() ,
,![]() ,
,![]() ;
;
(3)A:①过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,
,
![]() 轴,
轴,![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]()
![]()
![]()
![]() 的纵坐标为
的纵坐标为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,
,
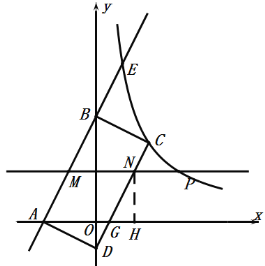
②当![]() 时,如图1,点
时,如图1,点![]() 与点
与点![]() 关于
关于![]() 轴对称,由轴对称的性质可得:点
轴对称,由轴对称的性质可得:点![]() 的坐标是
的坐标是![]() ;
;
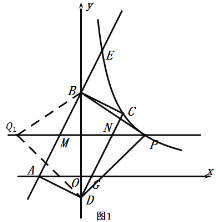
当![]() 时,如图2,过点
时,如图2,过点![]() 作
作![]() ⊥
⊥![]() 轴于
轴于![]() ,直线
,直线![]() 交
交 ![]() 轴于
轴于![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
点![]() 的坐标是
的坐标是![]() ,
,
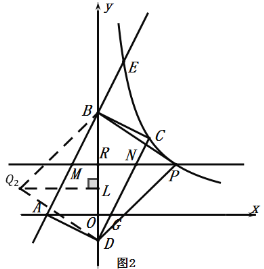
当![]() 时,如图3,点
时,如图3,点![]() 与点
与点![]() 关于
关于![]() 轴对称,由轴对称的性质可得:点
轴对称,由轴对称的性质可得:点![]() 的坐标是
的坐标是![]() ;
;
B:①过点![]() 作
作![]() 轴于点
轴于点![]()
![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 为菱形,
为菱形,![]() ,
,
∵![]() 轴,
轴,
∴ME∥BO,
∴![]() ,
,
![]() ,
,
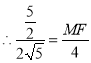 ,
,
![]() ,
,
![]() 的纵坐标为
的纵坐标为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ;
;
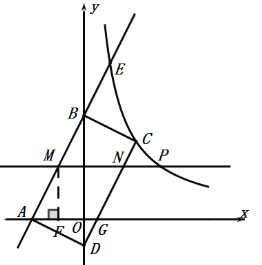
②当![]() 时,如图4,点
时,如图4,点![]() 与点
与点![]() 关于
关于![]() 轴对称,由轴对称的性质可得:点
轴对称,由轴对称的性质可得:点![]() 的坐标是
的坐标是![]() ;
;
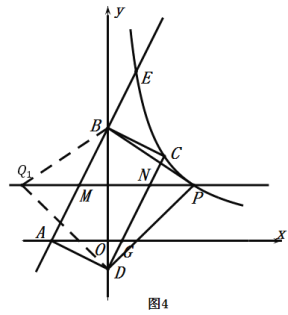
当![]() 时,如图5,过点
时,如图5,过点![]() 作
作![]() ⊥
⊥![]() 轴于
轴于![]() ,直线
,直线![]() 交
交 ![]() 轴于
轴于![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
点![]() 的坐标是
的坐标是![]() ,
,
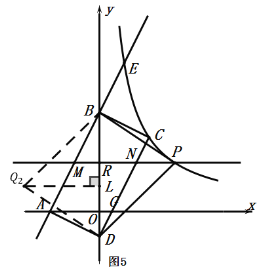
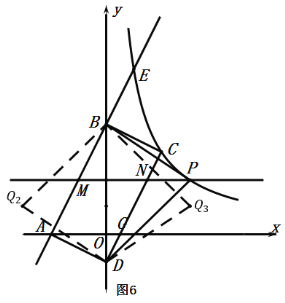
当![]() 时,如图6,点
时,如图6,点![]() 与点
与点![]() 关于
关于![]() 轴对称,由轴对称的性质可得:点
轴对称,由轴对称的性质可得:点![]() 的坐标是
的坐标是![]() ;
;


科目:初中数学 来源: 题型:
【题目】某校为了丰富学生课余生活,计划开设以下课外活动项目:A—版画,B—机器人,C—航模,D—园艺种植.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查(每位学生必须选且只能选一个项目),并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
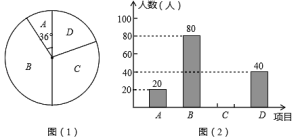
(1)这次被调查的学生共有 人;扇形统计图中,选“D—园艺种植”的学生人数所占圆心角的度数是 °
(2)请你将条形统计图补充完整;
(3)若该校学生总数为1000人,试估计该校学生中最喜欢“机器人”和最喜欢“航模”项目的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
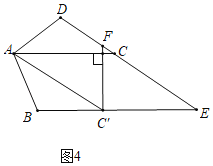
【题目】问题情境:在综合实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动,如图(1),将一张菱形纸片ABCD(∠BAD=60°)沿对角线AC剪开,得到△ABC和△ACD
操作发现:(1)将图(1)中的△ABC以A为旋转中心,顺时针方向旋转角α(0°<α<60°)得到如图(2)所示△ABC′,分别延长BC′和DC交于点E,发现CE=C′E.请你证明这个结论.
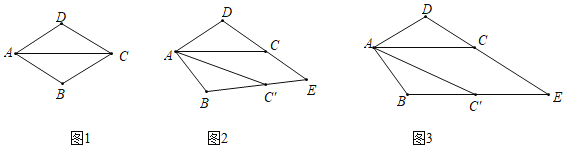
(2)在问题(1)的基础上,当旋转角α等于多少度时,四边形ACEC′是菱形?请你利用图(3)说明理由.
拓展探究:(3)在满足问题(2)的基础上,过点C′作C′F⊥AC,与DC交于点F.试判断AD、DF与AC的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,抛物线![]() (b为常数)的对称轴是直线x=1.
(b为常数)的对称轴是直线x=1.
(1)求该抛物线的表达式;
(2)点A(8,m)在该抛物线上,它关于该抛物线对称轴对称的点为A',求点A'的坐标;
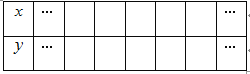
(3)选取适当的数据填入下表,并在如图5所示的平面直角坐标系内描点,画出该抛物线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() .顶点为
.顶点为![]() 的抛物线经过点
的抛物线经过点![]() .
.
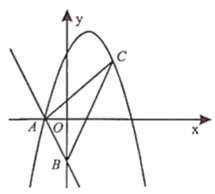
(1)求抛物线的解析式;
(2)点![]() 为第一象限抛物线上一动点.设点
为第一象限抛物线上一动点.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() .当
.当![]() 为何值时,
为何值时,![]() 的值最大,并求
的值最大,并求![]() 的最大值;
的最大值;
(3)在(2)的结论下,若点![]() 在
在![]() 轴上,
轴上,![]() 为直角三角形,请直接写出点
为直角三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
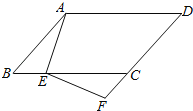
【题目】如图,在平行四边形ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
(1)求证:△ABE∽△ECF;
(2)若AB=5,AD=8,BE=2,求FD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P是一个反比例函数的图象与正比例函数y=﹣2x的图象的公共点,PQ垂直于x轴,垂足Q的坐标为(2,0).
(1)求这个反比例函数的解析式;
(2)如果点M在这个反比例函数的图象上,且△MPQ的面积为6,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
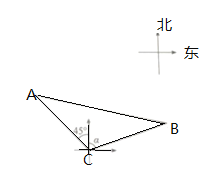
【题目】如图,从灯塔![]() 处观测轮船
处观测轮船![]() 的位置,测得轮船
的位置,测得轮船![]() 在灯塔
在灯塔![]() 北偏西
北偏西![]() 的方向,轮船
的方向,轮船![]() 在灯塔
在灯塔![]() 北偏东
北偏东![]() 的方向,且
的方向,且![]() 海里,
海里,![]() 海里,已知
海里,已知![]() ,求
,求![]() 、
、![]() 两艘轮船之间的距离.(结果保留根号)
两艘轮船之间的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据全等形的定义,我们把四个角分别相等,四条边分别相等的两个凸四边形叫做全等四边形.
(1)某同学在探究全等四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
①四条边成比例的两个凸四边形全等;( 命题)
②四个角分别相等的两个凸四边形全等;( 命题)
③两个面积相等的正方形全等;( 命题)
④三角分别相等,且其中两角夹边相等两个凸四边形全等.( 命题)
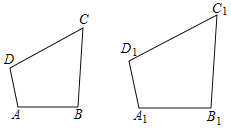
(2)如图,在四边形ABCD和四边形A1B1C1D1中,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,AB=A1B1,BC=∠B1C1,CD=C1D1.求证:在四边形ABCD和四边形A1B1C1D1全等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com