
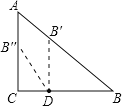
【题目】Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(如图).把△ABC绕着点D逆时针旋转m(0<m<180)度后,使点B恰好落在初始Rt△ABC的边上,得到△A'B'C',则有下列结论:①线段BD也绕点D逆时针旋转了m度;②点B′可能落在AB边上;③△ADA'为等边三角形;④m可能等于120.其中正确结论的序号是_____(把所有正确结论的序号都填在横线上)

【答案】①②④
【解析】
根据旋转的性质判断①②即可,通过计算可求出当B′在AC边上时,旋转角是120°,B′在AB边上时旋转角是80度,判断③④即可.
因为D为旋转中心,所以线段BD也绕点D逆时针旋转了m度,故①正确,
因为BD逆时针旋转,所以点B′可能落在AB边上,故②正确,
当B′在AB边上时,在线段AB取一点B′,使DB=DB′,在线段AC取一点B″,使DB=DB″,
∴①旋转角m=∠BDB′=180-∠DB′B-∠B=180°-2∠B=80°,
②当B″在AC边上时,在线段AC取一点B″,使DB=DB″,
在Rt△B″CD中,
∵DB″=DB=2CD,
∴∠CDB″=60°,
旋转角∠BDB″=180°-∠CDB″=120°.故④正确,
∵对应点与旋转中心所连线段的夹角对于旋转角,
∴∠ADA′即是旋转角,
∴△ADA′不是等边三角形,故③错误,
综上所述:①②④正确,
故答案为:①②④


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是

A. AB=![]() EF B. AB=2EF C. AB=
EF B. AB=2EF C. AB=![]() EF D. AB=
EF D. AB=![]() EF
EF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线相交于点0,AC=2,BD=![]() .将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的面积是( )
.将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的面积是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴相交于A(﹣3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
如图1,已知△ABC为等边三角形,点D,E分别在边AB、AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想:在图1中,线段PM与PN的数量关系是 ,∠MPN的度数是 ;
(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,
①判断△PMN的形状,并说明理由;
②求∠MPN的度数;
(3)拓展延伸:若△ABC为直角三角形,∠BAC=90°,AB=AC=10,点DE分别在边AB,AC上,AD=AE=4,连接DC,点M,P,N分别为DE,DC,BC的中点.把△ADE绕点A在平面内自由旋转,如图3,请直接写出△PMN面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°
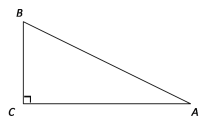
(1)尺规作图:作AC的垂直平分线,垂足为E,交AB于点D.(不写作法,保留作图痕迹,不证明)
(2)连结CD,求证: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“扶贫攻坚”活动中,城南中学计划选购甲、乙两种物品慰问贫困户.已知甲物品的单价比乙物品的单价高10元,若用500元单独购买甲物品与450元单独购买乙物品的数量相同.
(1)请问甲、乙两种物品的单价各为多少?
(2)如果该单位计划购买甲、乙两种物品共55件,总费用不少于5000元且不超过5020元,通过计算得出共有几种选购方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com