
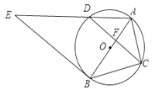
【题目】如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
(1)若CD=2![]() , AF=3,求⊙O的周长;
, AF=3,求⊙O的周长;
(2)求证:直线BE是⊙O的切线.
【答案】(1)8π;(2)证明见解析.
【解析】
(1)连接OC.设半径为r,在Rt△OFC中利用勾股定理即可解决问题.
(2)只要证明CD∥EB,即可得到∠AFD=∠ABE=90°,由此可以得出结论.
解:(1)连接OC.设半径为r,
∵OA⊥CD,
∴DF=FC=![]() ,
,
在RT△OFC中,∵∠OFC=90°,FC=![]() ,OF=r﹣3,OC=r,
,OF=r﹣3,OC=r,
∴r2=(r﹣3)2+(![]() )2 ,
)2 ,
∴r=4,
∴⊙O的周长为8π.
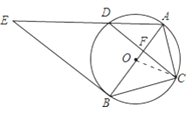
(2)证明:∵OA⊥CD,
∴DF=FC,AD=AC,∠AFD=90°
∴∠ADC=∠ACD,
∵∠E=∠ACD,
∴∠ADC=∠E,
∴CD∥EB,
∴∠AFD=∠ABE=90°,
∴BE是⊙O的切线.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=ax2+bx+c(a≠0,a≠c)过点A(1,0),顶点为 B,且抛物线不过第三象限.
(1)过点B作直线l垂直于x轴于点C,若点C坐标为(2,0),a=1,求b和c的值;
(2)比较![]() 与0的大小,并说明理由;
与0的大小,并说明理由;
(3)若直线y2=2x+m经过点B,且与抛物线交于另外一点D(![]() ,b+8),求当
,b+8),求当![]() ≤x<5时y1的取值范围.
≤x<5时y1的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两则材料,回答问题,材料一:定义直线y=ax+b与直线y=bx+a互为“互助直线”,例如,直线y=x+4与直y=4x+1互为“互助直线”;材料二:对于平面直角坐标系中的任意两点P1(x1,y1)、P2(x2,y2),P1、P2两点间的直角距离d(P1,P2)=|x1﹣x2|+|y1﹣y2|.如:Q1(﹣3,1)、Q2(2,4)两点间的直角距离为d(Q1,Q2)=|﹣3﹣2|+|1﹣4|=8;材料三:设P0(x0,y0)为一个定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离.
(1)计算S(﹣1,6),T(﹣2,3)两点间的直角距离d(S,T)= ;
(2)直线y=﹣2x+3上的一点H(a,b)又是它的“互助直线”上的点,求点H的坐标.
(3)对于直线y=ax+b上的任意一点M(m,n),都有点N(3m,2m﹣3n)在它的“互助直线”上,试求点L(5,﹣1)到直线y=ax+b的直角距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘,如图所示,AB与CD是水平的,BC与水平面的夹角为60°,其中AB=60cm,CD=40cm,BC=40cm,那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为___________cm

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级(1)班积极响应校团委的号召,每位同学都向“希望工程”捐献图书,全班40名同学共捐图书400册.特别值得一提的是李保、王刚两位同学在父母的支持下各捐献了90册图书.班长统计了全班捐书情况如下表(被粗心的马小虎用墨水污染了一部分):
册数 | 4 | 5 | 6 | 7 | 8 | 90 |
人数 | 6 | 8 | 15 | 2 |
(1)分别求出该班级捐献7册图书和8册图书的人数;
(2)请算出捐书册数的平均数、中位数和众数,并判断其中哪个统计量不能反映该班同学捐书册数的一般状况,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教科书中这样写道:“我们把多项式![]() 及
及![]() 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
例如:分解因式
![]() ;例如求代数式
;例如求代数式![]() 的最小值.
的最小值.![]() .可知当
.可知当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() ,根据阅读材料用配方法解决下列问题:
,根据阅读材料用配方法解决下列问题:
(1)分解因式:![]() _____
_____
(2)当![]() 为何值时,多项式
为何值时,多项式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
(3)当![]() 为何值时.多项式
为何值时.多项式![]() 有最小值并求出这个最小值
有最小值并求出这个最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() .
.
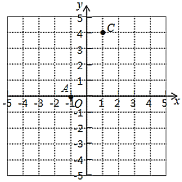
(1)求点![]() 的坐标;
的坐标;
(2)求![]() 的面积;
的面积;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 三点为顶点的三角形的面积为7?若存在,请直接写出点
三点为顶点的三角形的面积为7?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为坐标原点,A,B分别在y轴、x轴正半轴上,D是x轴正半轴上一动点,AD=DE,∠ADE=α,矩形AOBC的面积为32且AC=2BC.
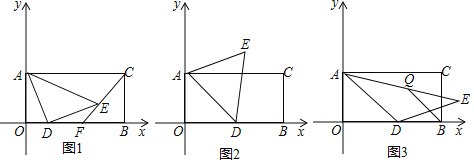
(1)如图1,当α=90°时,直线CE交x轴于点F,求证:F为OB中点;
(2)如图2,当α=60°时,若D是OB中点,求E点坐标;
(3)如图3,当α=120°时,Q是AE的中点,求D点运动过程中BQ的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com