
【题目】某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
成绩频数分布表
组别 | 成绩(分) | 频数 |
A | 50≤x<60 | 6 |
B | 60≤x<70 | m |
C | 70≤x<80 | 20 |
D | 80≤x<90 | 36 |
E | 90≤x<100 | n |

(1)频数分布表中的m= , n=;
(2)样本中位数所在成绩的级别是 , 扇形统计图中,E组所对应的扇形圆心角的度数是;
(3)若该校共有2000名学生,请你估计体育综合测试成绩不少于80分的大约有多少人?
【答案】
(1)4;18
(2)D;108
(3)
解:根据题意得:2000×(36%+30%)=1320(人),
答:该校九年级的学生中,测试成绩不少于80分的大约有132人
【解析】解:(1)∵20÷20%=100,且A占6%,
∴E占30%,
∴B占8%,
∴6÷6%=m÷8%,
∴m=8,18
∴n=18.
故答案为4,18;(2)样本中位数在36%部分,即为D部分,E组所对应的扇形圆心角的度数是360°× ![]() =108°,
=108°,
故答案为D,108°;
(1)根据频数分布表和扇形统计图可知E占30%,B占8%,即可得出B、D的频数;(2)根据中位数的概念,可得出中位数在D级别中,用360°乘以E组所占的比例即可;(3)用800乘以测验成绩不少于85分的所占的比例即可求出答案.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是正方形?给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片的一角斜折过去,点B落在点D处,EF为折痕,再把FC折过去与FD重合,FH为折痕,问:
(1)EF与FH有什么位置关系?
(2)∠CFH与∠BEF有什么数量关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
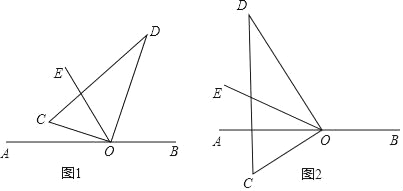
【题目】如图,直角三角板的直角顶点O在直线AB上,OC,OD是三角板的两条直角边,OE平分∠AOD.
(1)若∠COE=20°,则∠BOD= ;若∠COE=α,则∠BOD= (用含α的代数式表示)
(2)当三角板绕O逆时针旋转到图2的位置时,其它条件不变,试猜测∠COE与∠BOD之间有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )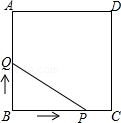
A.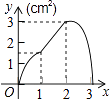
B.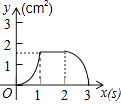
C.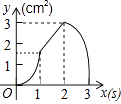
D.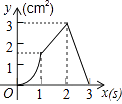
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,则下列叙述不正确的是( )

A. 点O不在直线AC上
B. 射线AB与射线BC是指同一条射线
C. 图中共有5条线段
D. 直线AB与直线CA是指同一条直线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,“回”字形的道路宽为1米,整个“回”字形的长为8米,宽为1米,一个人从入口点A沿着道路中央走到中点B,他共走了( )

A. 55米 B. 55.5米 C. 56米 D. 56.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(x>9且x<26,单位:km)

(1)说出这辆出租车每次行驶的方向.
(2)求经过连续4次行驶后,这辆出租车所在的位置.
(3)这辆出租车一共行驶了多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1, O为正方形ABCD的中心,分别延长OA,OD到点F,E,使OF=2OA,OE=2OD,连接EF,将△FOE绕点O按逆时针方向旋转角α得到△FOE,连接AE,BF(如图2).
(1)探究AE与BF的数量关系,并给予证明;
(2)当α=30°时,求证: △AOE为直角三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com