
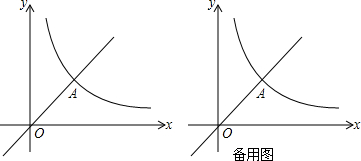
���� ��1���������⣬���Ƚ���A��1��1�����뼴�����˫���ߵĽ���ʽ����������ͼ�����x�ķ�Χ��
��2����ͼ����������������ۣ��ݴ˼��ɵý⣻
��3����������ȷ��4-a��ȡֵ��Χ�������ý⣮
��� �⣺��1������A��1��1������${y}_{1}=\frac{k}{x}$���ɵã�k=1��
��ͼ��֪��y1��y2ʱx��ȡֵ��Χ�ǣ�0��x��1��
��2�����ڵ�P��
���P��m��$\frac{1}{m}$����S��m��m��
�ٵ�0��m��1ʱ��PS=$\frac{1}{m}-m$��PQ=m��
������PQRS��������PQ=PS��
����m=$\frac{1}{m}-m$��
��ã�m=$\frac{\sqrt{2}}{2}$��m=$-\frac{\sqrt{2}}{2}$���ᣩ��
�ڵ�m��1ʱ��PS=$m-\frac{1}{m}$��PQ=m��
������PQRS��������PQ=PS��
����$m-\frac{1}{m}=m$��
��ʱ�⣻
��3����x=4-aʱ
y3=a��4-a��2��y2=4-a
��y3��y2
��a��4-a��2��4-a
��a��a-4��2+��a-4����0
[a��a-4��+1]��a-4����0
��a2-4a+1����a-4����0
��y2��y1
��x��1
��4-a��1
��a��3
��a-4��0
��a2-4a+1��0
��2-$\sqrt{3}$��a��2+$\sqrt{3}$
��2-$\sqrt{3}$��a��3
���� ������Ҫ�����˶��κ�����һ�κ����ͷ�����������ͼ�������ʣ����ۺ��ԱȽ�ǿ����Ŀ��Ҫע�������ܽᣮ


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
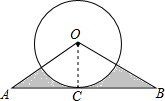 ��ͼ����OAB�У�OA=OB=4����A=30�㣬AB���O�����ڵ�C����ͼ����Ӱ���ֵ����������������У�
��ͼ����OAB�У�OA=OB=4����A=30�㣬AB���O�����ڵ�C����ͼ����Ӱ���ֵ����������������У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��֪A1��A2��A3����An��x���ϵĵ㣬��OA1=A1A2=A2A3=A3A4=��=An-1An=1���ֱ����A1��A2��A3����An����x��Ĵ��߽����κ���y=$\frac{1}{2}$x2��x��0����ͼ���ڵ�P1��P2��P3����Pn�����ǡ�OA1P1�����ΪS1������P1��P1B1��A2P2�ڵ�B1���ǡ�P1B1P2�����ΪS2������P2��P2B2��A3P3�ڵ�B2���ǡ�P2B2P3�����ΪS3�������ν�����ȥ����S3=$\frac{5}{4}$�����ǡ�Pn-1Bn-1Pn��n��1�������ΪSn����Sn==$\frac{2n-1}{4}$��
��ͼ��֪A1��A2��A3����An��x���ϵĵ㣬��OA1=A1A2=A2A3=A3A4=��=An-1An=1���ֱ����A1��A2��A3����An����x��Ĵ��߽����κ���y=$\frac{1}{2}$x2��x��0����ͼ���ڵ�P1��P2��P3����Pn�����ǡ�OA1P1�����ΪS1������P1��P1B1��A2P2�ڵ�B1���ǡ�P1B1P2�����ΪS2������P2��P2B2��A3P3�ڵ�B2���ǡ�P2B2P3�����ΪS3�������ν�����ȥ����S3=$\frac{5}{4}$�����ǡ�Pn-1Bn-1Pn��n��1�������ΪSn����Sn==$\frac{2n-1}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
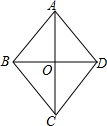 ��ͼ��������ABCD�У�AC��BD�ཻ�ڵ�O��AC=8��BD=6�������εı߳�AB���ڣ�������
��ͼ��������ABCD�У�AC��BD�ཻ�ڵ�O��AC=8��BD=6�������εı߳�AB���ڣ�������| A�� | 10 | B�� | $\sqrt{7}$ | C�� | 6 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪������C1��y=a1x2+b1x+c1��C2��y=a2x2+b2x+c2������ԭ�㣬����ֱ�ΪA��B����x�����һ����ֱ�ΪM��N�������A���B����M���N������ԭ��O�����ĶԳƣ����������C1��C2Ϊ���������ߣ�����д��һ�Խ���������C1��C2��ʹ�ı���ANBMǡ���Ǿ��Σ�����д��һ�������߽���ʽ��y=-$\sqrt{3}$x2+2$\sqrt{3}$x��y=$\sqrt{3}$x2+2$\sqrt{3}$x���𰸲�Ψһ����
��ͼ����֪������C1��y=a1x2+b1x+c1��C2��y=a2x2+b2x+c2������ԭ�㣬����ֱ�ΪA��B����x�����һ����ֱ�ΪM��N�������A���B����M���N������ԭ��O�����ĶԳƣ����������C1��C2Ϊ���������ߣ�����д��һ�Խ���������C1��C2��ʹ�ı���ANBMǡ���Ǿ��Σ�����д��һ�������߽���ʽ��y=-$\sqrt{3}$x2+2$\sqrt{3}$x��y=$\sqrt{3}$x2+2$\sqrt{3}$x���𰸲�Ψһ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
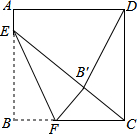 ��ͼ��������ABCD�ı߳���16����E�ڱ�AB�ϣ�AE=3����F�DZ�BC�ϲ����B��C�غϵ�һ�����㣬�ѡ�EBF��EF�۵�����B����B�䴦������CDB��ǡΪ���������Σ���DB��ij�Ϊ16��4$\sqrt{5}$��
��ͼ��������ABCD�ı߳���16����E�ڱ�AB�ϣ�AE=3����F�DZ�BC�ϲ����B��C�غϵ�һ�����㣬�ѡ�EBF��EF�۵�����B����B�䴦������CDB��ǡΪ���������Σ���DB��ij�Ϊ16��4$\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
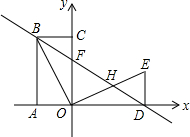 ��ͼ���ı���OABC�Ǿ��Σ���A��C���������ϣ���ODE�ǡ�OCB�Ƶ�O˳ʱ����ת90��õ��ģ���D��x���ϣ�ֱ��BD��y���ڵ�F����OE�ڵ�H���߶�BC��OC�ij��Ƿ���x2-6x+8=0������������OC��BC��
��ͼ���ı���OABC�Ǿ��Σ���A��C���������ϣ���ODE�ǡ�OCB�Ƶ�O˳ʱ����ת90��õ��ģ���D��x���ϣ�ֱ��BD��y���ڵ�F����OE�ڵ�H���߶�BC��OC�ij��Ƿ���x2-6x+8=0������������OC��BC���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com