【题目】如图，E是ABCD的边CD的中点，延长AE交BC的延长线于点F．
（1）求证：△ADE≌△FCE．
（2）若∠BAF=90°，BC=5，EF=3，求CD的长．
【答案】（1）证明过程见解析；（2）8.
【解析】试题分析：（1）由平行四边形的性质得出AD∥BC，AB∥CD，证出∠DAE=∠F，∠D=∠ECF，由AAS证明△ADE≌△FCE即可；（2）由全等三角形的性质得出AE=EF=3，由平行线的性质证出∠AED=∠BAF=90°，由勾股定理求出DE，即可得出CD的长．
试题解析：（1）∵四边形ABCD是平行四边形， ∴AD∥BC，AB∥CD，
∴∠DAE=∠F，∠D=∠ECF， ∵E是ABCD的边CD的中点， ∴DE=CE，
在△ADE和△FCE中，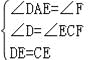
，∴△ADE≌△FCE（AAS）；
（2）∵ADE≌△FCE， ∴AE=EF=3， ∵AB∥CD， ∴∠AED=∠BAF=90°，
在ABCD中，AD=BC=5， ∴DE=
=
=4， ∴CD=2DE=8
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】方程也可以用来解决一些几何问题，如图，P为△ABC内一点，连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F，则把△ABC分成六个小三角形，其中四个小三角形面积已在图上标明，设△BPD的面积为
，△CPE的面积为
，
（1）
；
（填数字）；
（2）求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．
（1）如图1，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．求证：中点四边形EFGH是平行四边形；
（2）如图2，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH的形状，并证明你的猜想；
（3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，直接写出中点四边形EFGH的形状．（不必证明）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在某超市小明买了1千克甲种糖果和2千克乙种糖果，共付38元；小强买了2千克甲种糖果和0.5千克乙种糖果，共付27元．
（1）求该超市甲、乙两种糖果每千克各需多少元？
（2）某顾客到该超市购买甲、乙两种糖果共20千克混合，欲使总价不超过240元，问该顾客混合的糖果中甲种糖果最少多少千克？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
