
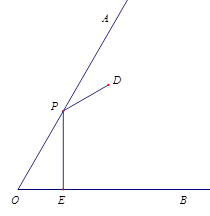
【题目】如图,已知∠AOB=60°,点P为射线OA上的一个动点,过点P作PE⊥OB,交OB 于点E,点D在∠AOB内,且满足∠DPA=∠OPE,DP+PE=6.
(1)当DP=PE时,求DE的长;
(2)在点P的运动过程中,请判断是否存在一个定点M,使得![]() 的值不变?并证明你的判断.
的值不变?并证明你的判断.
【答案】(1)DE=3![]() ;(2)当M点在射线OA上且满足OM=2
;(2)当M点在射线OA上且满足OM=2![]() 时,
时,![]() 的值不变,始终为1.理由见解析.
的值不变,始终为1.理由见解析.
【解析】
(1)作PF⊥DE交DE于F.由直角三角形的两锐角互余得到∠OPE=30°,在由平角的定义,得出∠EPD=120°.然后解三角形DPE即可得出结论.
(2)当点P与点M不重合时,延长EP到K使得PK=PD.可以证明△KPM≌△DPM,得到MK=MD.作ML⊥OE于L,MN⊥EK于N.解Rt△MLO得到ML的长,易证四边形MNEL为矩形,得到EN=ML=3.通过证明MK=ME,得到ME=MK=MD,即可得到![]() =1.
=1.
当点P与点M重合时,结论也成立.
(1)作PF⊥DE交DE于F.

∵PE⊥BO,∠AOB=60°,∴∠OPE=30°,∴∠DPA=∠OPE=30°,∴∠EPD=120°.
∵DP=PE,DP+PE=6,∴∠PDE=30°,PD=PE=3,∴DF=PDcos30°=![]() ,∴DE=2DF=
,∴DE=2DF=![]() .
.
(2)当M点在射线OA上且满足OM=![]() 时,
时,![]() 的值不变,始终为1.理由如下:
的值不变,始终为1.理由如下:
①当点P与点M不重合时,延长EP到K使得PK=PD,连接MK.
∵∠DPA=∠OPE,∠OPE=∠KPA,∴∠KPA=∠DPA,∴∠KPM=∠DPM.
∵PK=PD,PM是公共边,∴△KPM≌△DPM,∴MK=MD.
作ML⊥OE于L,MN⊥EK于N.
∵MO=![]() ,∠MOL=60°,∴ML=MOsin60°=3.
,∠MOL=60°,∴ML=MOsin60°=3.
∵PE⊥BO,ML⊥OE,MN⊥EK,∴四边形MNEL为矩形,∴EN=ML=3.
∵EK=PE+PK=PE+PD=6,∴EN=NK.
∵MN⊥EK,∴MK=ME,∴ME=MK=MD,即![]() =1.
=1.

②当点P与点M重合时,由上述过程可知结论成立.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某中学开展“绿化家乡、植树造林”活动,为了解全校植树情况,对该校甲、乙、丙、
丁四个班级植树情况进行了调查,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,完成下列问题:
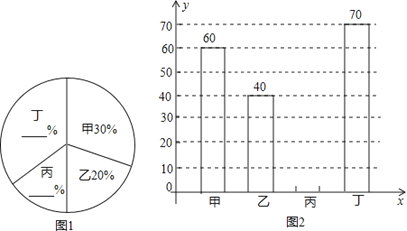
(1)这四个班共植树 棵;
(2)请你在答题卡上补全两幅统计图;
(3)求图1中“甲”班级所对应的扇形圆心角的度数;
(4)若四个班级植树的平均成活率是95%,全校共植树2000棵,请你估计全校种植的树中成活的树有多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
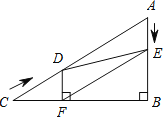
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的外接圆,连结OA、OB、OC,延长BO与AC交于点D,与
的外接圆,连结OA、OB、OC,延长BO与AC交于点D,与![]() 交于点F,延长BA到点G,使得
交于点F,延长BA到点G,使得![]() ,连接FG.
,连接FG.
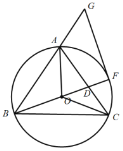

备用图
(1)求证:FG是![]() 的切线;
的切线;
(2)若![]() 的半径为4.
的半径为4.
①当![]() ,求AD的长度;
,求AD的长度;
②当![]() 是直角三角形时,求
是直角三角形时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形 ABCD 中,AD∥BC,AB=BC,对角线 AC、BD 交于点 O,BD 平分∠ABC,过点 D 作 DE⊥BC 交 BC 的延长线于点 E.连接 OE.
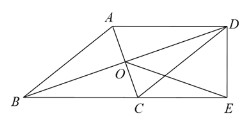
(1)求证:四边形 ABCD 是菱形;
(2)若 tan∠DBC=![]() ,AB=
,AB=![]() ,求线段 OE 的长.
,求线段 OE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格中,点A、B均为格点.
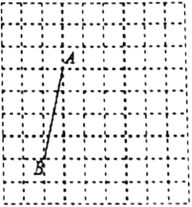
(Ⅰ)AB的长等于_____.
(Ⅱ)若点C是以AB为底边的等腰直角三角形的顶点,点D在边AC上,且满足S△ABD=![]() S△ABC.请在如图所示的网格中,用无刻度的直尺,画出线段BD,并简要说明点D的位置是如何找到的(不要求证明)______.
S△ABC.请在如图所示的网格中,用无刻度的直尺,画出线段BD,并简要说明点D的位置是如何找到的(不要求证明)______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-![]() x2+bx+c,与
x2+bx+c,与![]() 轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
(Ⅰ)求抛物线的解析式及点D的坐标;
(Ⅱ)点![]() 是抛物线上的动点,当
是抛物线上的动点,当![]() 时,求点F坐标;
时,求点F坐标;
(Ⅲ)若点P是x轴上方抛物线上的动点,以PB为边作正方形PBFG,随着点P的运动,正方形的大小、位置也随着改变,当顶点F或G恰好落在y轴上时,请直接写出点P的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
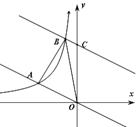
【题目】如图,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]()
![]() 在第二象限内的图象相交于点
在第二象限内的图象相交于点![]() ,将直线
,将直线![]() 向上平移后与反比例函数图象在第二象限内交于点
向上平移后与反比例函数图象在第二象限内交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() 的面积为3,则直线
的面积为3,则直线![]() 的关系式为:________
的关系式为:________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com