
���� ��1�������꼶��3��Ϊ����������ݳ����˱ʼDZ�x�����������ľߺУ�x+4�����������ܼ�=���ۡ�������Ϲ������м���Ʒ������290Ԫ�����ɵó�����x��һԪһ�η��̣���֮���ɵó����ۣ�
��2�����ٹ���Ľ�Ʒ���ܼ۸�ΪmԪ�������Żݷ����ɷֱ�����ڼס��ҳ��й�������֧�����ܷ��ã��ȽϺɵó����ۣ�
��� �⣺��1�������꼶��3��Ϊ����������ݳ����˱ʼDZ�x�����������ľߺУ�x+4������
��������ã�10x+12��x+4��=290��
��ã�x=11��
��x+4=15��
�����꼶��3��Ϊ����������ݳ�����11���ʼDZ���15���ľߺУ�
��2�����ٹ���Ľ�Ʒ���ܼ۸�ΪmԪ��
��������ã��׳����ܷ��ã�290+m����0.9=0.9m+261��
�ҳ����ܷ��ã�290+m-200����0.8+200=0.8m+272��
��0.9m+261��0.8m+272ʱ��m��110��
��0.9m+261=0.8m+272ʱ��m=110��
��0.9m+261��0.8m+272ʱ��m��110��
�������������ֹ������Ʒ�ܼ۵���110Ԫʱ��ѡ��׳��л��㣻���ֹ������Ʒ�ܼ۵���110Ԫʱ��ѡ�����ҳ��з�����ͬ�����ֹ������Ʒ�ܼ۸���110Ԫʱ��ѡ���ҳ��л��㣮
���� ���⿼����һԪһ�η��̵�Ӧ���Լ�һԪһ�β���ʽ��Ӧ�ã�����Ĺؼ��ǣ���1�������ܼ�=���ۡ�������Ϲ������м���Ʒ������290Ԫ���г�����x��һԪһ�η��̣���2�������Żݷ����ɷֱ�����ڼס��ҳ��й�������֧�����ܷ��ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
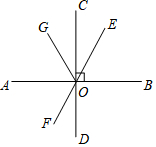 ��ͼ��ֱ��AB��CD��EF�ཻ�ڵ�O��AB��CD��OGƽ�֡�AOE�������FOD=28�㣬��ô��AOG=59�ȣ�
��ͼ��ֱ��AB��CD��EF�ཻ�ڵ�O��AB��CD��OGƽ�֡�AOE�������FOD=28�㣬��ô��AOG=59�ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -4��-3 | B�� | 4��3 | C�� | 6��1 | D�� | -6��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
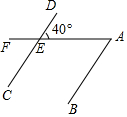 ��ͼ��ֱ��AB��CD��AF��CD�ڵ�E����DEF=140�㣬���A�Ķ����ǣ�������
��ͼ��ֱ��AB��CD��AF��CD�ڵ�E����DEF=140�㣬���A�Ķ����ǣ�������| A�� | 140�� | B�� | 40�� | C�� | 50�� | D�� | 60�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com