
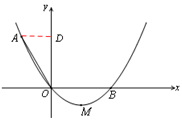
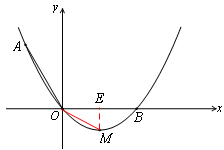
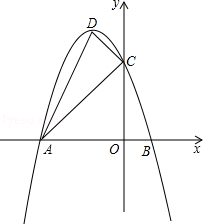
 经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=1200.
经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=1200.
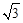 。
。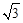 )。
)。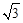 ),B(2,0)代入
),B(2,0)代入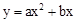 ,得:
,得: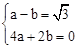 ,解得
,解得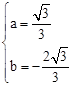 。
。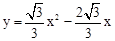 。
。
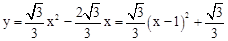 。
。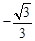 ),即OE=1,EM=
),即OE=1,EM=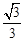 。
。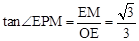 。∴
。∴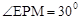 。
。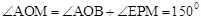 。
。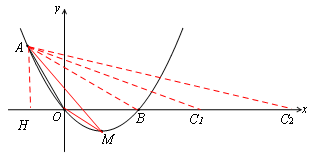
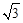 ,HB=HO+OB=3,
,HB=HO+OB=3,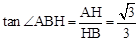 。
。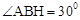 ,∴
,∴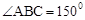 。
。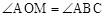 。
。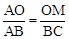 ,或②
,或②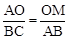 。
。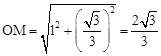 ,
,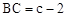 ,
,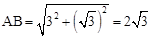 。
。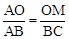 得,
得,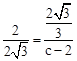 ,解得
,解得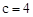 。∴C1(4,0)。
。∴C1(4,0)。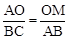 得,
得,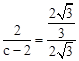 ,解得
,解得 。∴C2(8,0)。
。∴C2(8,0)。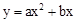 ,即可求得a、b,从而求得抛物线的表达式。
,即可求得a、b,从而求得抛物线的表达式。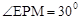 ,进而求得∠AOM的大小。
,进而求得∠AOM的大小。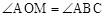 ,根据相似三角形的判定,分
,根据相似三角形的判定,分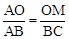 ,
,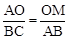 两种情况讨论。
两种情况讨论。

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源:不详 题型:单选题
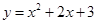 绕着原点旋转180°,所得抛物线的解析式是( ).
绕着原点旋转180°,所得抛物线的解析式是( ).| A.y=-(x-1)2-2 | B.y=-(x+1)2-2 |
C.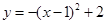 | D.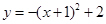 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| x | 3000 | 3200 | 3500 | 4000 |
| y | 100 | 96 | 90 | 80 |
| 租出的车辆数 | | 未租出的车辆数 | |
| 租出每辆车的月收益 | | 所有未租出的车辆每月的维护费 | |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 中,点O为原点,点B在反比例函数
中,点O为原点,点B在反比例函数 (
( >
> )图象上,△BOC的面积为
)图象上,△BOC的面积为 .
.
 的关系式;
的关系式;  个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用
个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用 表示,求出S关于t的函数关系式,并求出当运动时间t取何值时,△BEF的面积最大?
表示,求出S关于t的函数关系式,并求出当运动时间t取何值时,△BEF的面积最大?  秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
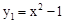 交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C.
交x轴的正半轴于点A,交y轴于点B,将此抛物线向右平移4个单位得抛物线y2,两条抛物线相交于点C.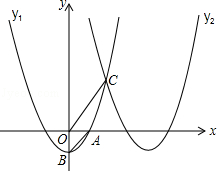
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
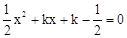 .
. 的图象与x轴的两个交点A、B间的距离为4时,求此二次函数的解析式;
的图象与x轴的两个交点A、B间的距离为4时,求此二次函数的解析式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
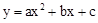 图象上部分点的坐标满足下表:
图象上部分点的坐标满足下表:| x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
| y | … | ﹣3 | ﹣2 | ﹣3 | ﹣6 | ﹣11 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com