
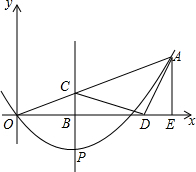
 ��ͼ����ƽ��ֱ������ϵ�У���֪������y=ax2+bx�ĶԳ���Ϊx=$\frac{3}{4}$���Ҿ�����A��2��1������P���������ϵĶ��㣬P�ĺ�����Ϊm��0��m��2��������P��PB��x�ᣬ����ΪB��PB��OA�ڵ�C����O����ֱ��PB�ĶԳƵ�ΪD������CD��AD������A��AE��x�ᣬ����ΪE��
��ͼ����ƽ��ֱ������ϵ�У���֪������y=ax2+bx�ĶԳ���Ϊx=$\frac{3}{4}$���Ҿ�����A��2��1������P���������ϵĶ��㣬P�ĺ�����Ϊm��0��m��2��������P��PB��x�ᣬ����ΪB��PB��OA�ڵ�C����O����ֱ��PB�ĶԳƵ�ΪD������CD��AD������A��AE��x�ᣬ����ΪE������ ��1�����������߶Գ��ṫʽ�ʹ��뷨�ɵù���a��b�ķ����飬�ⷽ����ɵ������ߵĽ���ʽ��
��2������OA���ڵ�ֱ�߽���ʽΪy=kx������A��2��1���������OA���ڵĽ���ʽΪy=$\frac{1}{2}$x����ΪPC��x�ᣬ����C�ú�������P�ĺ�������ͬ��Ϊm����x=m����y=$\frac{1}{2}$m�����Եó���C��m��$\frac{1}{2}$m�����ֵ�O��D����ֱ��PB�ĶԳƣ��������е����깫ʽ�ɵõ�D�ĺ�����Ϊ2m�����D������Ϊ��2m��0����
����ΪO��D����ֱ��PB�ĶԳƣ�����PB��ֱƽ��OD����CO=CD����Ϊ����ACD���ܳ�=AC+CD+AD=AC+CO+AD=AO��AO=$\sqrt{O{E}^{2}+A{E}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$�����Ե�AD��Сʱ����ACD���ܳ���С�����ݴ��߶���̣���֪��ʱ��D��E�غϣ��������Ϊ2����m=1��
��3�����д��ߵó�CD=OC���ٽ�OC��AC��AD��m��ʾ��Ȼ���������۷ֱ�õ�����m�ķ��̣����m���ٸ�����֪����ѡȡ��������ĵ�P���꼴�ɣ�
��� �⣺��1�������⣬��$\left\{\begin{array}{l}{-\frac{b}{2a}=\frac{3}{4}}\\{4a+2b=1}\end{array}\right.$�����$\left\{\begin{array}{l}{a=1}\\{b=-\frac{3}{2}}\end{array}\right.$
��y=x2-$\frac{3}{2}$x
��2��C��m��$\frac{1}{2}$m����D��2m��0����m=1
��3�������⣬��B��m��0��
��Rt��OBC��OC2=OB2+BC2=m2+$��\frac{1}{2}m��^{2}$=$\frac{5}{4}$m2��
��OC=$\frac{\sqrt{5}}{2}$m �֡�O��D����ֱ��PC�Գƣ�
��CD=OC=$\frac{\sqrt{5}}{2}$m
��Rt��AOE��OA=$\sqrt{{OE}^{2}{+AE}^{2}}$=$\sqrt{{2}^{2}{+1}^{2}}$=$\sqrt{5}$
��AC=OA-OC=$\sqrt{5}$-$\frac{\sqrt{5}}{2}$m
��Rt��ADE��AD2=AE2+DE2=12+��2-2m��2=4m2-8m+5
������������ۣ�
����AC=CD����$\sqrt{5}$-$\frac{\sqrt{5}}{2}$m=$\frac{\sqrt{5}}{2}$m�����m=1����P��1��$-\frac{1}{2}$��
����AC=AD������AC2=AD2����5-5m+$\frac{5}{4}$m2=4m2-8m+5
���m1=0��m2=$\frac{12}{11}$����0��m��2����m=$\frac{12}{11}$����P��$\frac{12}{11}$��$-\frac{54}{121}$��
����DA=DC������DA2=DC2����4m2-8m+5=$\frac{5}{4}$m2
���m1=$\frac{10}{11}$��m2=2���ߣ�0��m��2����m=$\frac{10}{11}$����P��$\frac{10}{11}$��$-\frac{65}{121}$��
��������������ACDΪ����������ʱ����P������ֱ�ΪP1��1��$-\frac{1}{2}$����P2��$\frac{12}{11}$��$-\frac{54}{121}$����P3��$\frac{10}{11}$��$-\frac{65}{121}$����
���� ���⿴�����κ������ۺ����ã�����ϵ������������ʽ�����ĶԳƣ���ֱƽ���ߵ����ʣ����������ε����ʣ�����������˼�룮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �������� | B�� | ������ | C�� | ������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��AOB=60�㣬��P�ڱ�OA�ϣ�OP=20����M��N�ڱ�OB�ϣ�PM=PN����MN=4����OM����8��
��ͼ����֪��AOB=60�㣬��P�ڱ�OA�ϣ�OP=20����M��N�ڱ�OB�ϣ�PM=PN����MN=4����OM����8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4cm��5cm��11cm | B�� | 4cm��5cm��8cm | C�� | $\sqrt{3}$cm��$\sqrt{2}$cm��$\sqrt{5}$cm | D�� | 2cm��3cm��6cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | һ | �� | �� | �� | �� |
| �ù�Ʊÿ���ǵ� | +4 | +4.5 | -1 | -2.5 | -6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x4+x4=x16 | B�� | ��-2a��2=-4a2 | C�� | x7��x5=x2 | D�� | m2•m3=m6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
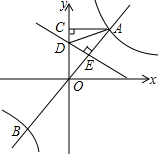 ��ͼ����ԭ��O��ֱ��AB�뷴��������y=$\frac{k}{x}$��k��0����ͼ����A��B���㣬��B����Ϊ��-2��m��������A��AC��y���ڵ�C��OA�Ĵ�ֱƽ����DE��OC�ڵ�D����AB�ڵ�E������ACD���ܳ�Ϊ5����k��ֵΪ6��
��ͼ����ԭ��O��ֱ��AB�뷴��������y=$\frac{k}{x}$��k��0����ͼ����A��B���㣬��B����Ϊ��-2��m��������A��AC��y���ڵ�C��OA�Ĵ�ֱƽ����DE��OC�ڵ�D����AB�ڵ�E������ACD���ܳ�Ϊ5����k��ֵΪ6���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com