
����Ŀ����ͼ1�������㳡װ�з��ܡ�̫���ܷ���ķ�⻥������·�ƣ��Ƹ˶���װ�з�����������м�װ��̫���ܰ壬�¶�װ��·�ƣ���ϵͳ����������ijһʱ�̵Ľ���ͼ��ͼ2����֪̫���ܰ��֧��BC��ֱ�ڵƸ�OF��·�ƶ���E�������6�ף�DE=1.8�ף���CDE=60�㣮�Ҹ������еĵ���λ���趨̫���ܰ�AB����б��Ϊ43�㣮AB=1.5�ף�CD=1�ף�Ϊ��֤��Ϊ1�ķ��������ҶƬ���ϰ���ȫ��ת����ҶƬ��̫���ܰ嶥��A��������벻������0.5�ף���Ƹ�OF����Ҫ��ߣ������ÿ�ѧ�����������sin43����0.6820��cos43����0.7314��tan43����0.9325�����������λС����
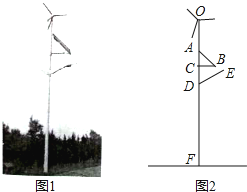
���𰸡��Ƹ�OF����Ҫ7.70m��
��������
�����������E��EG��������G����D��DH��EG��H����Rt��ABC�У����AC=ABcos��CAB��1.10������CDE=60�㣬�õ�EH=![]() DE=0.9���ó�DF=GH=EG��EH=6��0.9=5.1������OF=0.5+1.10+1+5.1=7.70m��
DE=0.9���ó�DF=GH=EG��EH=6��0.9=5.1������OF=0.5+1.10+1+5.1=7.70m��
�⣺��E��EG��������G����D��DH��EG��H��

��DF=HG��
��Rt��ABC��AC=ABcos��CAB=1.5��cos43��=1.5��0.7314��1.10��
�ߡ�CDE=60�㣬
���EDH=30�㣬
��EH=![]() DE=0.9��
DE=0.9��
��DF=GH=EG��EH=6��0.9=5.1��
��OF=OA+AC+CD+DF=0.5+1.10+1+5.1=7.70m��
�𣺵Ƹ�OF����Ҫ7.70m��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OA��OB��AB��x���ڵ�C����A��![]() ��1���ڷ���������
��1���ڷ���������![]() ��ͼ���ϣ�
��ͼ���ϣ�
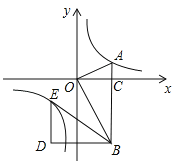
��1����������![]() �ı���ʽ��
�ı���ʽ��
��2����x��ĸ������ϴ���һ��P��ʹ��S��AOP=![]() S��AOB�����P�����ꣻ
S��AOB�����P�����ꣻ
��3��������BOA�Ƶ�B����ʱ�뷽����ת60���õ���BDE��ֱ��д����E�����꣬���жϵ�E�Ƿ��ڸ÷�����������ͼ���ϣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
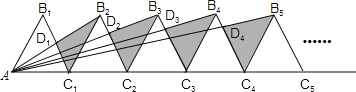
����Ŀ����ͼ��n+1���߳�Ϊ2�ĵȱ���������һ������ͬһֱ���ϣ�����B2D1C1�����ΪS1����B3D2C2�����ΪS2��������Bn+1DnCn�����ΪSn����S2= ��Sn= �����ú�n��ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧ�ٰ���һ�������ҵ��й�����Ϊ������ݽ����������ȷ��7��ͬѧ�μӾ��������ǵľ����ɼ�������ͬ��������Ѿ�֪���Լ��ijɼ������ܷ��ǰ�������������������7��ͬѧ�ɼ���______________������ƽ��������������������λ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��3��x��2��2��5��y�ύ������Ϊ��������
A. ��0��2�� B. ��0����5�� C. ��0��7�� D. ��0��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
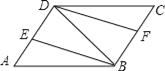
����Ŀ����ͼ����ABCD�У����ӶԽ���BD��BEƽ�֡�ABD��AD�ڵ�E��DFƽ�֡�BDC��BC�ڵ�F��
��1����֤����AEB�ա�CFD��
��2����BD=BA�����ж��ı���DEBF����״��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
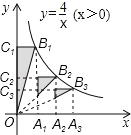
����Ŀ����ͼ����A1��A2��A3��x���ϣ���OA1=A1A2=A2A3���ֱ����A1��A2��A3��y���ƽ���ߣ��뷴��������![]() ��ͼ��ֱ��ڵ�B1��B2��B3���ֱ����B1��B2��B3��x���ƽ���ߣ��ֱ���y�ύ�ڵ�C1��C2��C3������OB1��OB2��OB3����ôͼ����Ӱ���ֵ����֮��Ϊ ��
��ͼ��ֱ��ڵ�B1��B2��B3���ֱ����B1��B2��B3��x���ƽ���ߣ��ֱ���y�ύ�ڵ�C1��C2��C3������OB1��OB2��OB3����ôͼ����Ӱ���ֵ����֮��Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
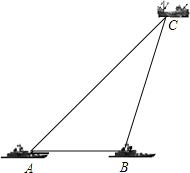
����Ŀ����ͼ�����ҹ����㵺���������������������еĺ��ബA��B��B����A����������������������10����ľ��룬ijһʱ�������ബͬʱ�����A�Ķ�������B�ı�ƫ��15�㷽����һ�����������洬C�����ʱ�洬C�뺣�ബB�ľ����Ƕ��٣�������������ţ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com