
ΓΨΧβΡΩΓΩ»γΆΦΘ§ «“Μ÷÷–±ΩφΑϋΘ§ΤδΩφ¥χ”…ΥΪ≤ψ≤ΩΖ÷ΓΔΒΞ≤ψ≤ΩΖ÷ΚΆΒςΫΎΩέΙΙ≥…Θ°ά÷ά÷”ΟΚσΖΔœ÷Θ§Ά®ΙΐΒςΫΎΩέΦ”≥ΛΜρΥθΕΧΒΞ≤ψ≤ΩΖ÷ΒΡ≥ΛΕ»Θ§Ω…“‘ ΙΩφ¥χΒΡ≥ΛΕ»Θ®ΒΞ≤ψ≤ΩΖ÷”κΥΪ≤ψ≤ΩΖ÷≥ΛΕ»ΒΡΚΆΘ§Τδ÷–ΒςΫΎΩέΥυ’ΦΒΡ≥ΛΕ»Κω¬‘≤ΜΦΤΘ©‘ω≥ΛΜρΥθΕΧΘ°Ψ≠≤βΝΩΘ§ΒΟΒΫ»γœ¬ ΐΨίΘΚ
ΒΞ≤ψ≤ΩΖ÷ΒΡ≥ΛΕ»Θ®cmΘ© | Γ≠ | 4 | 6 | 8 | 10 | Γ≠ | 150 |
ΥΪ≤ψ≤ΩΖ÷ΒΡ≥ΛΕ»Θ®cmΘ© | Γ≠ | 73 | 72 | 71 | ΓΓ ΓΓ | Γ≠ | 0 |
Θ®1Θ©ΗυΨί…œ±μ÷– ΐΨίΒΡΙφ¬…Θ§Χν–¥±μΗώ÷–Ω’ΑΉ¥ΠΒΡ ΐΨίΘΜ
Θ®2Θ©…ηΒΞ≤ψ≤ΩΖ÷ΒΡ≥ΛΕ»ΈΣxcmΘ§«κ”ΟΚ§xΒΡ¥ζ ΐ Ϋ±μ Ψ≥ωΥΪ≤ψ≤ΩΖ÷ΒΡ≥ΛΕ»ΓΓ ΓΓcmΘΜ
Θ®3Θ©ΗυΨίά÷ά÷ΒΡ…μΗΏΚΆœΑΙΏΘ§Ωφ¥χΒΡ≥ΛΕ»ΈΣ110cm ±Θ§±≥Τπά¥Ήν φ Θ§«κ«σ≥ω¥Υ ±ΒΞ≤ψ≤ΩΖ÷ΒΡ≥ΛΕ»Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©70ΘΜΘ®2Θ©yΘΫ©¹![]() x+75cmΘΜΘ®3Θ©70cm
x+75cmΘΜΘ®3Θ©70cm
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΙφ¬…Φ¥Ω…ΒΟ≥ωΫαΙϊΘΜ
Θ®2Θ©Ιέ≤λ±μΗώΩ…÷ΣΘ§y «xΒΡ“Μ¥ΈΚ· ΐΘ§…ηyΘΫkx+bΘ§άϊ”Ο¥ΐΕ®œΒ ΐΖ®Φ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®3Θ©Ν–≥ωΖΫ≥ΧΦ¥Ω…ΫβΨωΈ ΧβΘ°
ΫβΘΚΘ®1Θ©ΗυΨίΒΞ≤ψ≤ΩΖ÷ΒΡ≥ΛΕ»ΟΩ‘ωΦ”2cmΘ§ΥΪ≤ψ≤ΩΖ÷ΒΡ≥ΛΕ»Φθ–Γ1cmΘ§Ω…ΒΟΒ±ΒΞ≤ψ≤ΩΖ÷ΒΡ≥ΛΕ»ΈΣ10cm ±Θ§ΥΪ≤ψ≤ΩΖ÷ΒΡ≥ΛΕ»ΈΣ70Θ°
Ι ¥πΑΗΈΣΘΚ70ΘΜ
Θ®2Θ©Ιέ≤λ±μΗώΩ…÷ΣΘ§y «xΒΡ“Μ¥ΈΚ· ΐΘ§…ηyΘΫkx+bΘ§
‘ρ”–![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ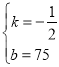 Θ§
Θ§
ΓύyΘΫ©¹![]() x+75Θ°
x+75Θ°
Ι ¥πΑΗΈΣΘΚyΘΫ©¹![]() x+75ΘΜ
x+75ΘΜ
Θ®3Θ©ΗυΨίΧβ“βΒΟΘΚ
![]() Θ§
Θ§
ΫβΒΟxΘΫ70Θ°
¥πΘΚΩφ¥χΒΡ≥ΛΕ»ΈΣ110cm ±Θ§ΒΞ≤ψ≤ΩΖ÷ΒΡ≥ΛΕ»ΈΣ70cmΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§÷±œΏ![]() ΙΐΒψ
ΙΐΒψ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ΘΚ
ΘΚ![]() ”κ÷±œΏ
”κ÷±œΏ![]() ΫΜ”ΎΒψBΘ§”κx÷αΫΜ”ΎΒψCΘ°
ΫΜ”ΎΒψBΘ§”κx÷αΫΜ”ΎΒψCΘ°
Θ®1Θ©«σkΒΡ÷ΒΘΜ
Θ®2Θ©ΚαΓΔΉίΉχ±ξΕΦ «’ϊ ΐΒΡΒψΫ–Ήω’ϊΒψΘ°
ΔΌ Β±b=4 ±Θ§÷±Ϋ”–¥≥ωΓςOBCΡΎΒΡ’ϊΒψΗω ΐΘΜ
ΔΎ»τΓςOBCΡΎΒΡ’ϊΒψΗω ΐ«Γ”–4ΗωΘ§ΫαΚœΆΦœσΘ§«σbΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
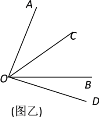
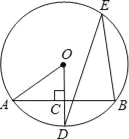
ΓΨΧβΡΩΓΩ‘ΡΕΝœ¬Οφ≤ΡΝœΘΚ ΐ―ßΩΈ…œΘ§άœ ΠΗχ≥ωΝΥ»γœ¬Έ ΧβΘΚ»γΆΦΦΉΘ§ΓœAOB=70ΓψΘ§OCΤΫΖ÷ΓœAOBΘ°
»τΓœBOD=20ΓψΘ§«κΡψ≤Ι»ΪΆΦ–ΈΘ§≤Δ«σΓœCODΒΡΕ» ΐΘ°
“‘œ¬ «–ΓΟςΒΡΫβ¥πΙΐ≥ΧΘΚ
ΫβΘΚ»γΆΦ““Θ§“ρΈΣOCΤΫΖ÷ΓœAOBΘ§ΓœAOB=70ΓψΘ§
Υυ“‘ΓœBOC=____ΓœAOB=________ΓψΘ°
“ρΈΣΓœBOD=20ΓψΘ§
Υυ“‘ΓœCOD= ΓψΘ°
–ΓΨ≤ΥΒΘΚΓΑΈ“ΨθΒΟ’βΗωΧβ”–ΝΫ÷÷«ιΩωΘ§–ΓΟςΩΦ¬«ΒΡ «OD‘ΎΓœAOBΆβ≤ΩΒΡ«ιΩωΘ§ ¬ Β…œΘ§ODΜΙΩ…Ρή‘ΎΓœAOBΒΡΡΎ≤ΩΓ± Θ°
Άξ≥…“‘œ¬Έ ΧβΘΚ
Θ®1Θ©«κΡψΫΪ–ΓΟςΒΡΫβ¥πΙΐ≥Χ≤Ι≥δΆξ’ϊΘΜ
Θ®2Θ©ΗυΨί–ΓΨ≤ΒΡœκΖ®Θ§«κΡψ‘ΎΆΦΦΉ÷–Μ≠≥ωΝμ“Μ÷÷«ιΩωΕ‘”ΠΒΡΆΦ–ΈΘ§«σ≥ω¥Υ ±ΓœCODΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΥΡΒψAΓΔBΓΔCΓΔDΘ°
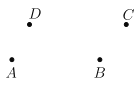
Θ®1Θ©”Ο‘≤ΙφΚΆΈόΩΧΕ»ΒΡ÷±≥ΏΑ¥œ¬Ν–“Σ«σ”κ≤Ϋ÷ηΜ≠≥ωΆΦ–ΈΘΚ
ΔΌΜ≠÷±œΏABΘ°
ΔΎΜ≠…δœΏDCΘ°
Δέ―”≥ΛœΏΕΈDA÷ΝΒψEΘ§ Ι![]() Θ°(±ΘΝτΉςΆΦΚέΦΘ)
Θ°(±ΘΝτΉςΆΦΚέΦΘ)
ΔήΜ≠“ΜΒψPΘ§ ΙΒψPΦ»‘Ύ÷±œΏAB…œΘ§”÷‘ΎœΏΕΈCE…œΘ°
Θ®2Θ©‘ΎΘ®1Θ©÷–ΥυΜ≠ΆΦ–Έ÷–Θ§»τ![]() cmΘ§
cmΘ§![]() cmΘ§ΒψFΈΣœΏΕΈDEΒΡ÷–ΒψΘ§«σAFΒΡ≥ΛΘ°
cmΘ§ΒψFΈΣœΏΕΈDEΒΡ÷–ΒψΘ§«σAFΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
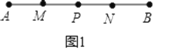
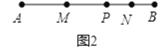
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΒψP «œΏΕΈAB…œΒΡ“ΜΒψΘ§ΒψMΓΔNΖ÷±π «œΏΕΈAPΓΔPBΒΡ÷–ΒψΘ°
Θ®1Θ©»γΆΦ1Θ§»τΒψP «œΏΕΈABΒΡ÷–ΒψΘ§«“MP=4cmΘ§«σœΏΕΈABΒΡ≥ΛΘΜ
Θ®2Θ©»γΆΦ2Θ§»τΒψP «œΏΕΈAB…œΒΡ»Έ“ΜΒψΘ§«“AB=12cmΘ§«σœΏΕΈMNΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§AB «Γ―OΒΡ“ΜΧθœ“Θ§ODΓΆABΘ§¥ΙΉψΈΣCΘ§ΫΜΓ―O”ΎΒψDΘ§ΒψE‘ΎΓ―O…œΘ°
Θ®1Θ©»τΓœAOD=52ΓψΘ§«σΓœDEBΒΡΕ» ΐΘΜ
Θ®2Θ©»τOC=3Θ§OA=5Θ§«σABΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
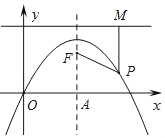
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏy=©¹x2+2xΒΡΕ‘≥Τ÷α”κx÷αΫΜ”ΎΒψAΘ§ΒψF‘Ύ≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œΘ§«“ΒψFΒΡΉίΉχ±ξΈΣ![]() Θ°Ιΐ≈ΉΈοœΏ…œ“ΜΒψPΘ®mΘ§nΘ©œρ÷±œΏy=
Θ°Ιΐ≈ΉΈοœΏ…œ“ΜΒψPΘ®mΘ§nΘ©œρ÷±œΏy=![]() Ής¥ΙœΏΘ§¥ΙΉψΈΣMΘ§Ν§ΫαPFΘ°
Ής¥ΙœΏΘ§¥ΙΉψΈΣMΘ§Ν§ΫαPFΘ°
Θ®1Θ©Β±m=2 ±Θ§«σ÷ΛΘΚPF=PMΘΜ
Θ®2Θ©Β±ΒψPΈΣ≈ΉΈοœΏ…œ»Έ“β“ΜΒψ ±Θ§PF=PM «ΖώΜΙ≥…ΝΔΘΩ»τ≥…ΝΔΘ§«κΗχ≥ω÷ΛΟςΘΜ»τ≤Μ≥…ΝΔΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥Ρξ5‘¬Θ§Έ“ΙζΡœΖΫΡ≥ ΓAΓΔBΝΫ –‘β ή―œ÷ΊΚιά‘‘÷ΚΠΘ§1.5Άρ»Υ±ΜΤ»ΉΣ“ΤΘ§ΝΎΫϋœΊ –CΓΔDΜώ÷ΣAΓΔBΝΫ –Ζ÷±πΦ±–ηΨ»‘÷ΈοΉ 200Ε÷ΚΆ300Ε÷ΒΡœϊœΔΚσΘ§ΨωΕ®Βς‘ΥΈοΉ ÷ß‘°‘÷«χΘ°“―÷ΣC –”–Ψ»‘÷ΈοΉ 240Ε÷Θ§D –”–Ψ»‘÷ΈοΉ 260Ε÷Θ§œ÷ΫΪ’β–©Ψ»‘÷ΈοΉ »Ϊ≤ΩΒςΆυAΓΔBΝΫ –Θ°“―÷Σ¥”C –‘ΥΆυAΓΔBΝΫ –ΒΡΖ―”ΟΖ÷±πΈΣΟΩΕ÷20‘ΣΚΆ25‘ΣΘ§¥”D –‘ΥΆυΆυAΓΔBΝΫ –ΒΡΖ―”Ο±πΈΣΟΩΕ÷15‘ΣΚΆ30‘ΣΘ§…η¥”D –‘ΥΆυB –ΒΡΨ»‘÷ΈοΉ ΈΣxΕ÷Θ°
Θ®1Θ©«κΧν–¥œ¬±μ
AΘ®Ε÷Θ© | BΘ®Ε÷Θ© | ΚœΦΤΘ®Ε÷Θ© | |
C | ΓΓ ΓΓ | ΓΓ ΓΓ | 240 |
D | ΓΓ ΓΓ | x | 260 |
ΉήΦΤΘ®Ε÷Θ© | 200 | 300 | 500 |
Θ®2Θ©…ηCΓΔDΝΫ –ΒΡΉή‘ΥΖ―ΈΣw‘ΣΘ§«σw”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωΉ‘±δΝΩxΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©Ψ≠Ιΐ«ά–όΘ§¥”D –ΒΫB –ΒΡ¬ΖΩωΒΟΒΫΝΥΗΡ…ΤΘ§ΥθΕΧΝΥ‘Υ δ ±ΦδΘ§‘ΥΖ―ΟΩΕ÷Φθ…Όm‘ΣΘ®mΘΨ0Θ©Θ§Τδ”ύ¬ΖœΏ‘ΥΖ―≤Μ±δΘ°»τCΓΔDΝΫ –ΒΡΉή‘ΥΖ―ΒΡΉν–Γ÷Β≤Μ–Γ”Ύ10320‘ΣΘ§«σmΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΑΈε“ΜΓ±ΤΎΦδΘ§–ΓΟς“ΜΦ“≥ΥΉχΗΏΧζ«ΑΆυΡ≥ –¬Ο”ΈΘ§ΦΤΜ°ΒΎΕΰΧλΉβ”Ο–¬Ρή‘¥Τϊ≥ΒΉ‘Φί≥ω”ΈΓΘ
 [ά¥
[ά¥
ΗυΨί“‘…œ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©…ηΉβ≥Β ±ΦδΈΣ![]() –Γ ±Θ§Ήβ”ΟΦΉΙΪΥΨΒΡ≥ΒΥυ–ηΖ―”ΟΈΣ
–Γ ±Θ§Ήβ”ΟΦΉΙΪΥΨΒΡ≥ΒΥυ–ηΖ―”ΟΈΣ![]() ‘ΣΘ§Ήβ”Ο““ΙΪΥΨΒΡ≥ΒΥυ–ηΖ―”ΟΈΣ
‘ΣΘ§Ήβ”Ο““ΙΪΥΨΒΡ≥ΒΥυ–ηΖ―”ΟΈΣ![]() ‘ΣΘ§Ζ÷±π«σ≥ω
‘ΣΘ§Ζ÷±π«σ≥ω![]() Θ§
Θ§![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΚ· ΐ±μ¥ο ΫΘΜ
ΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®2Θ©«κΡψΑο÷ζ–ΓΟςΦΤΥψ≤Δ―Γ‘ώΡΡΗω≥ω”ΈΖΫΑΗΚœΥψΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com