如图.图形旋转一定角度后能与自身重合.则旋转的角度可能是 [ ] A．20° B．30° C．60° D．90° 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

如图，图形旋转一定角度后能与自身重合，则旋转的角度可能是

[　　]

A．20°

B．30°

C．60°

D．90°

答案：C

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

如图a，△ABC和△CEF是两个大小不等的等边三角形（等边三角形为三条边相等，三个角为60°的三角形），且有一个公共顶点C，点F、B、C在同一直线上，连接AF和BE．
（1）线段AF和BE有怎样的大小关系（写出结论，不需要说明理由）；
（2）将图a中的△CEF绕点C旋转一定的角度，得到图b，（1）中的结论还成立吗？作出判断并说明理由；
（3）若将图a中的△ABC绕点C旋转一定的角度，请你画出一个变换后的图形c（草图即可）．（1）中的结论还成立吗？作出判断不必说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

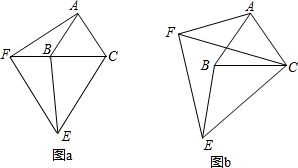
27、在平面内，如果一个图形绕一个定点旋转一定的角度后能与自身重合，那么就称这个图形是旋转对称图形，转动的这个角称为这个图形的一个旋转角．例如：正方形绕着它的对角线的交点旋转90°后能与自身重合（如图），所以正方形是旋转对称图形，它有一个旋转角为90度．
（1）判断下列命题的真假（在相应的括号内填上“真”或“假”）．
①等腰梯形是旋转对称图形，它有一个旋转角为180度．（

假

）
②矩形是旋转对称图形，它有一个旋转角为180°．（

真

）
（2）填空：下列图形中，是旋转对称图形，且有一个旋转角为120°的是

①，③

（写出所有正确结论的序号）：①正三角形；②正方形；③正六边形；④正八边形．
（3）写出两个多边形，它们都是旋转对图形，都有一个旋转角为72°，并且分别满足下列条件
①是轴对称图形，但不是中心对称图形：

如正五边形、正十五边形

；
②既是轴对称图形，又是中心对称图形：

如正十边形、正二十边形

．

查看答案和解析>>

科目：初中数学 来源： 题型：

我们容易发现：反比例函数的图象是一个中心对称图形．你可以利用这一结论解决问题．如图，在同一直角坐标系中，正比例函数的图象可以看作是：将x轴所在的直线绕着原点O逆时针旋转α度角后的图形．若它与反比例函数y=

的图象分别交于第一、三象限的点B、D，已知点A（-m，0）、C（m，0）．
（1）直接判断并填写：不论α取何值，四边形ABCD的形状一定是

平行四边形

；
（2）当点B为（p，1）时，四边形ABCD是矩形，直接写出p、α、和m的值；
（3）试探究：四边形ABCD能不能是菱形？若能，直接写出B点的坐标，若不能，说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

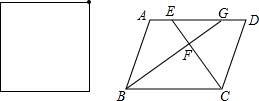（1）在如图的正方形中，以右上角顶点为旋转中心，按逆时针旋转一定角度后使之与原图形成轴对称，其中对称轴是原图形的某条边，并指出这时旋转角为多少度．
（2）在平行四边形ABCD中，∠BCD的平分线CE交AD于E，∠ABC的平分线BG

交CE于F，交AD于G．试说明：AE=DG．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图1，将射线OX绕点O按逆时针旋转n°的角，得到射线OY，如果点P为射线OY上一点，且OP=a，那么我们就规定用（a，n°）表示点P在平面内的位置，并记为P（a，n°）．例如在图2中，如果OM=6，∠XOM=200°，那么点M在平面内的位置记为M（6，200°）．
根据上述规定解答下列问题：
（1）在图3中，如果点N在平面内的位置记为N（10，35°），那么ON=

，∠XON=

°．
（2）将图3中的射线OY绕点O旋转一定的角度（小于360度），使得旋转后所得到的射线OZ与射线OY垂直，则旋转后点N在平面内的位置可记为

（10，125°）或（10，305°）

，请在图3中画出旋转后的图形．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学