
����Ŀ��С�����ݻ�ʦ����꼶�²�̲�P37ѧϰ���ݣ��Ժ���y= ![]() x2��ͼ������ʽ�����̽�����Խ������в������Ĺ��̲���������
x2��ͼ������ʽ�����̽�����Խ������в������Ĺ��̲��������� 
��1���Ա���x��ȡֵ��Χ��ȫ��ʵ����x��y�ļ����Ӧ��ֵ�����
x | �� | ��4 | n | ��2 | ��1 | 0 | 1 | 2 | 3 | 4 | �� |
y | �� | 8 | 4.5 | 2 | 0.5 | 0 | 0.5 | 2 | 4.5 | 8 | �� |
����n=��
��2����ͼ����ƽ��ֱ������������ϵxOy�У�����������ϱ��еIJ�����ֵΪ����ĵ㣬��������ĵ㣬�����ú����Ĵ���ͼ��
��3�����ݻ����ĺ���ͼ��С���۲췢�֣��ú�������Сֵ��û�����ֵ��������ֵȡ��Сʱ���Ա���x��ֵΪ ��
��4����һ��̽��������ͼ���֣� ������A��xa �� ya������B��xb �� yb���ں���y= ![]() ��ͼ���ϣ�
��ͼ���ϣ�
��xa��xb��0ʱ��ya��yb�Ĵ�С��ϵ����
��0��xa��xbʱ��ya��yb�Ĵ�С��ϵ����
��ֱ��y1ǡ�þ���������ͼ���ϵĵ㣨��2��2���루1��0.5������y��y1ʱ��x��ȡֵ��Χ�� ��
���𰸡�
��1��-3
��2���⣺��ͼ
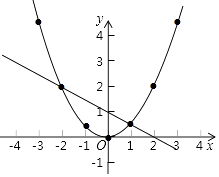
��3��0
��4��ya��yb�� ya��yb����2��x��1
���������⣺��1����y= ![]() x2=4.5ʱ��x=��3��
x2=4.5ʱ��x=��3��
��n=��3��
���Դ��ǣ���3��
����㡢���ߣ���������ͼ��
�ǹ۲캯��ͼ���֪�������ߵĶ�������Ϊ��0��0����
�൱x=0ʱ��yȡ��Сֵ��
���Դ��ǣ�0��
�Ȣٹ۲캯��ͼ���֪����x��0ʱ��yֵ��xֵ���������С����x��0ʱ��yֵ��xֵ�����������
�൱xa��xb��0ʱ��ya��yb����0��xa��xbʱ��ya��yb��
���Դ��ǣ�ya��yb��ya��yb��
����ͼ�л���ֱ��y1���۲캯��ͼ���֪������2��x��1ʱ��ֱ�����������Ϸ���
�൱y��y1ʱ��x��ȡֵ��Χ�ǩ�2��x��1��
���Դ��ǣ���2��x��1��
�����㾫�������ö��κ�����ͼ��Ͷ��κ��������ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���P��x����·���y���Ҳ࣬�ҵ�x��ľ���Ϊ5����y�����Ϊ1�����P������Ϊ�� ��
A. (1,-5) B. (5,1) C. (-1,5) D. (5,-1)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������һ��·��ͳ�Ƶ�ijʱ�����������ij�����������
���٣�km/h�� | 48 | 49 | 50 | 51 | 52 |
������������ | 5 | 4 | 8 | 2 | 1 |
���������ٵ���λ���������ֱ��ǣ� ��
A.50��8
B.50��50
C.49��50
D.49��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ȷ��ӳij����10��˾��1�·ݺ�ȥ�����ͷ��ã��ұ��ڱȽϣ���ôѡ������ʡ�ֱ�۵�ͳ��ͼ�ǣ�������
A. ͳ�Ʊ�B. ����ͳ��ͼC. ����ͳ��ͼD. ����ͳ��ͼ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������OABC�Ķ���O������ԭ���غϣ���߳�Ϊ2����A����C�ֱ���![]() �ᣬ
�ᣬ![]() ����������ϣ�����
����������ϣ�����![]() ��ͼ����CB���ڵ�D������
��ͼ����CB���ڵ�D������![]() ��
��![]() ������
Ϊ������![]() ����ͼ����D����AB���ڵ�E���뺯��
����ͼ����D����AB���ڵ�E���뺯��![]() ��ͼ���ڵ��������ڽ��ڵ�F������AF��EF��
��ͼ���ڵ��������ڽ��ڵ�F������AF��EF��

��1������![]() �ı���ʽ����ֱ��д��E��F��������꣮
�ı���ʽ����ֱ��д��E��F��������꣮
��2������AEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�����������һ���ڽ���120������ô��������������_____���Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���ABC=90�㣬AB=3��BC=4��CD=5��DA=5 ![]() ����BD�ij�Ϊ ��
����BD�ij�Ϊ �� 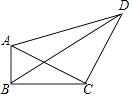
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ����60���������ֽƬ����ȥ���60��Ǻõ�һ���ı��Σ����1+��2= �� 
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com