
【题目】如图,正方形ABCD中,P是对角线BD上一点,连接AP、![]() ,BF⊥AP于H,CP、BH延长线分别交AD边于点E、F。
,BF⊥AP于H,CP、BH延长线分别交AD边于点E、F。
(1)求证:∠DAP=∠DCE
(2)求证:AE=FD
(3)猜想∠APE与∠FBD的数量关系,并说明理由.

【答案】(1)见解析;(2)见解析;(3)![]() ,理由见解析
,理由见解析
【解析】
(1)证明△ADP≌△CDP,根据全等三角形的对应角相等即可得∠DAP=∠DCE;
(2)证明ΔABF≌ΔDCE,根据全等三角形的对应边相等可得AF=DE,继而可证得答案;
(3)猜想:∠APE=2∠FBD,连接AC,由△ADP≌△CDP,可得AP=CP,继而可推导得出∠APE=2∠ACP,然后再证明∠FBD=∠ECA即可得到.
(1)∵四边形ABCD是正方形,
∴AD=CD,∠ADP=∠CDP,
在△ADP和△CDP中,
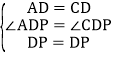 ,
,
∴△ADP≌△CDP,
∴∠DAP=∠DCE;
(2)∵四边形ABCD是正方形,
∴∠BAD=∠ADC=90°,AB=DC,
∴∠ABF+∠AFB=90°,
∵AP⊥BF,
∴∠AHF=90°,
∴∠HAF+ ∠AFB=90°,
∴∠ABF= ∠HAF,
∵∠DAP= ∠DCE,
∴∠ABF=∠DCE,
在ΔABF和ΔDCE中
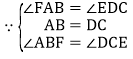 ,
,
∴ΔABF≌ΔDCE,
∴AF=DE,
∴AF+EF=DE+EF,
即AE=FD;
(3)猜想:∠APE=2∠FBD,理由如下:
连接AC,
由(1)知:△ADP≌△CDP,
∴AP=CP,
∴∠PAC=∠PCA,
∴∠APE=2∠ACP,
∵四边形ABCD是正方形,
∴∠ABD=∠DCA=45°,
∴∠ABD-∠ABF=∠DCA-∠DCE,
即∠FBD=∠ECA,
∴∠APE=2∠FBD.


科目:初中数学 来源: 题型:
【题目】如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )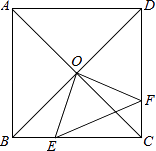
A.
B.
C.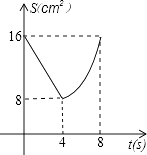
D.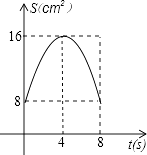
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有分别标有数字1,2,3,4四个小球,除数字不同外,小球没有任何区别,每次实验先搅拌均匀.
(1)若从中任取一球,球上的数字为偶数的概率为多少?
(2)若从中任取一球(不放回),再从中任取一球,请用画树状图或列表格的方法求出两个球上的数字之和为偶数的概率.
(3)若设计一种游戏方案:从中任取两球,两个球上的数字之差的绝对值为1为甲胜,否则为乙胜,请问这种游戏方案设计对甲、乙双方公平吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BDE中,∠BDE=90°,BD=6 ![]() ,点D的坐标是(7,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为 .
,点D的坐标是(7,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为 . 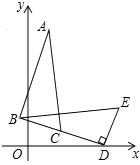
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°

(1)作边AB的垂直平分线交AB于点D,交BC于点E(尺规作图,不写作法,保留作图痕迹).
(2)连接AE,求证:AE=2DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣2的图象与x轴交于A、B两点,与y轴交于点C,点A的坐标为(4,0),且当x=﹣2和x=5时二次函数的函数值y相等.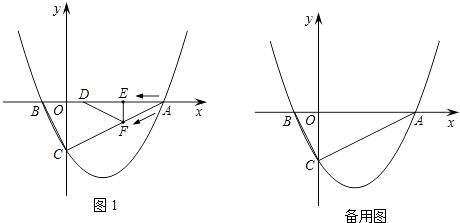
(1)求实数a、b的值;
(2)如图1,动点E、F同时从A点出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒 ![]() 个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.
个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.
①是否存在某一时刻t,使得△DCF为直角三角形?若存在,求出t的值;若不存在,请说明理由.
②设△DEF与△ABC重叠部分的面积为S,求S关于t的函数关系式;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com