
����Ŀ������ԭ�ͣ���ͼ�����ڵ���ֱ��������ABC�У���ACB=90����BC=a������AB�Ƶ�B˳ʱ����ת90���õ��߶�BD������CD������D����BCD��BC���ϵĸ�DE�� ��֤��ABC�ա�BDE���Ӷ��õ���BCD�����Ϊ![]() ��
��
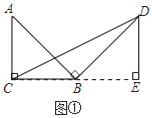
����̽������ͼ������Rt��ABC�У���ACB=90����BC=a������AB�Ƶ�B˳ʱ����ת90���õ��߶�BD������CD���ú�a�Ĵ���ʽ��ʾ��BCD���������˵�����ɣ�
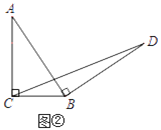
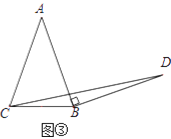
��Ӧ�ã���ͼ�����ڵ���������ABC�У�AB=AC��BC=a������AB�Ƶ�B˳ʱ����ת90���õ��߶�BD������CD��ֱ��д����BCD����������ú�a�Ĵ���ʽ��ʾ��
���𰸡�������
���������������:(1)����̽��:��ͼ��,����D��BC�Ĵ���,��BC���ӳ��߽��ڵ�E,�ɴ�ֱ�����ʾͿ��Եó���ABC�ա�BDE,����DE=BC=a,�����������ε������ʽ�ó�����,
(2)������:��ͼ��,����A��AF��BC��F,����D��DE��BC���ӳ����ڵ�E,�ɵ��������ε����ʿ��Եó�BF=![]() BC,���������Եó���AFB�ա�BED�Ϳ��Եó�BF=DE,�������ε������ʽ�Ϳ��Եó�����.
BC,���������Եó���AFB�ա�BED�Ϳ��Եó�BF=DE,�������ε������ʽ�Ϳ��Եó�����.
�������:(1)��BCD�����Ϊ![]() ,
,
����:��ͼ��,����D��BC�Ĵ���,��BC���ӳ��߽��ڵ�E,

���BED=��ACB=90��,
���߶�AB�Ƶ�B˳ʱ����ת90���õ��߶�BE,
��AB=BD,��ABD=90��,
���ABC+��DBE=90��,
�ߡ�A+��ABC=90��,
���A=��DBE,
�ڡ�ABC�͡�BDE��,
 ,
,
���ABC�ա�BDE��AAS��,
��BC=DE=a,
��S��BCD= ![]()
��S��BCD=![]() ,
,
(2)��Ӧ��:��ͼ��,����A��AF��BC��F,����D��DE��BC���ӳ����ڵ�E,
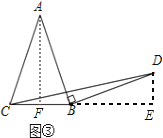
���AFB=��E=90��,BF= ![]() ,
,
���FAB+��ABF=90��,
�ߡ�ABD=90��,
���ABF+��DBE=90��,
���FAB=��EBD,
���߶�BD�����߶�AB��ת�õ���,
��AB=BD,
�ڡ�AFB�͡�BED��,
 ,
,
���AFB�ա�BED��AAS��,
��BF=DE= ![]() ,
,
��S��BCD= ![]() ,
,
��S��BCD=![]() ,
,
���BCD�����Ϊ![]() ,
,


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijװ���̣��ס������˿��Ժ�����ɣ����ס������˺���4��������Ҷ���12�������ɣ���֪����ÿ����Ҫ����580Ԫ���Ҷ���ÿ�������280Ԫ�����ҵ�����ɵ������Ǽ������������2����
��1���ס������˵���������̸�������죿
��2���������Ҫ����18����ɣ�Ӧ��ΰ��ż������˵Ĺ���ʹ����̱Ƚ�ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8�֣�ij�ֲ��ž����������е�349����ֻ��ܺ�295�����ֻ��ܴ���A��B����������50�����ڷ���ӭ��������࣮��֪����һ��A����������ֻ���8�裬���ֻ���4�裻����һ��B����������ֻ���5�裬���ֻ���9�裮
��l��ijУ2015����꼶ij�����С��н�����������ʹ��䷽������ƣ��ʷ�������Ĵ��䷽���м��֣����������Ƴ�����
��2��������һ��A�����͵ijɱ���200Ԫ������һ��B�����͵ijɱ���360Ԫ����˵����1�������ַ����ɱ���ͣ���ͳɱ��Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������AOB�У���AOB=90�㣬OA=3��OB=4������AOB��x�������Ե�A��B��OΪ��ת����˳ʱ����ת���ֱ�õ�ͼ����ͼ������������ת�õ���ͼ����ֱ�Ƕ��������Ϊ_______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
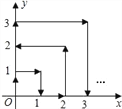
����Ŀ����ͼ��ʾһ���ʵ��ڵ�һ�����ڼ�x�ᡢy�����˶����ڵ�һ��������ԭ���ƶ���(0,1)�㣬������Ű�ͼ��ʾ��x�ᣬy��ƽ�еķ����˶�����ÿ���ƶ�һ����λ���ȣ���ô�ʵ��˶�����(n,n)��nΪ����������λ��ʱ���ô���ʽ��ʾ���õ�ʱ��Ϊ_________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڿ����еĴ����ٶ�v(m/s)���¶�T(��)�Ĺ�ϵ���±���
�¶�/�� | 0 | 5 | 10 | 15 | 20 |
�ٶ�v/(m/s) | 331 | 334 | 337 | 340 | 343 |
(1)д���ٶ�v���¶�T֮��Ĺ�ϵʽ��
(2)��T��30��ʱ���������Ĵ����ٶȣ�
(3)�������Ĵ����ٶ�Ϊ346m/sʱ���¶��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ��⡣
��1������2����1��|�� ![]() |+��3.14����0+4cos45��
|+��3.14����0+4cos45��
��2����֪x2��2x��7=0����x��2��2+��x+3����x��3����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ACD�͡�BCE���ǵ���ֱ�������Σ���ACD����BCE��90�㣬AE��DC��F��BD�ֱ�CE��AE�ڵ�G��H.�Բ²��߶�AE��BD��λ�ú�������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AB=3��BC=6����E�ڱ�BC�ϣ���BE=2CE���������ع���E��ֱ���۵�����C��D�Ķ�Ӧ��ֱ�ΪC�䡢D�䣬�ۺ����AD���ڵ�F������B��C�䡢D��ǡ����ͬһֱ����ʱ��AF�ij�Ϊ ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com