
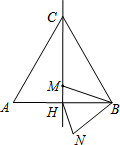
 如图,边长为4a的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )
如图,边长为4a的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )| A. | 2a | B. | a | C. | $\frac{1}{2}$a | D. | $\frac{1}{3}$a |
分析 取CB的中点G,连接MG,根据等边三角形的性质可得BH=BG,再求出∠HBN=∠MBG,根据旋转的性质可得MB=NB,然后利用“边角边”证明∴△MBG≌△NBH,再根据全等三角形对应边相等可得HN=MG,然后根据垂线段最短可得MG⊥CH时最短,再根据∠BCH=30°求解即可.
解答 解:如图,取BC的中点G,连接MG,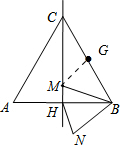
∵旋转角为60°,
∴∠MBH+∠HBN=60°,
又∵∠MBH+∠MBC=∠ABC=60°,
∴∠HBN=∠GBM,
∵CH是等边△ABC的对称轴,
∴HB=$\frac{1}{2}$AB,
∴HB=BG,
又∵MB旋转到BN,
∴BM=BN,
在△MBG和△NBH中,$\left\{\begin{array}{l}{BG=BH}\\{∠MBG=∠NBH}\\{MB=NB}\end{array}\right.$,
∴△MBG≌△NBH(SAS),
∴MG=NH,
根据垂线段最短,MG⊥CH时,MG最短,即HN最短,
此时∵∠BCH=$\frac{1}{2}$×60°=30°,CG=$\frac{1}{2}$AB=$\frac{1}{2}$×4a=2a,
∴MG=$\frac{1}{2}$CG=$\frac{1}{2}$×2a=a,
∴HN=a.
故选:B.
点评 本题考查了旋转的性质,等边三角形的性质,全等三角形的判定与性质,垂线段最短的性质,作辅助线构造出全等三角形是解题的关键,也是本题的难点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
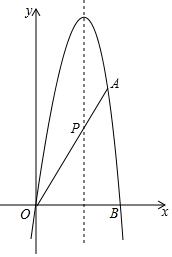 抛物线y=-$\sqrt{3}$x2+bx+c经过点O(0,0),A(4,4$\sqrt{3}$),与x轴的另一交点为点B,且抛物线的对称轴与线段OA交于点P.
抛物线y=-$\sqrt{3}$x2+bx+c经过点O(0,0),A(4,4$\sqrt{3}$),与x轴的另一交点为点B,且抛物线的对称轴与线段OA交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
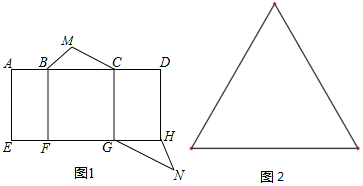
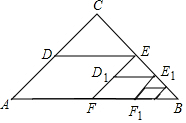 如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2,照此规律作下去,则S1=1,S2017=$\frac{1}{{4}^{2016}}$.
如图,△ABC中,∠C=90°,AC=BC=2,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2,照此规律作下去,则S1=1,S2017=$\frac{1}{{4}^{2016}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com