
【题目】如图,AB是⊙O的直径,点C、D是圆上两点,且OD∥AC,OD与BC交于点E.
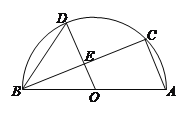
(1)求证:E为BC的中点;
(2)若BC=8,DE=3,求AB的长度.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)、根据直径所对的圆周角为直角可得∠C=90°,根据OD∥AC得出OD⊥BC,从而根据垂径定理得出E为BC的中点;(2)、根据垂径定理得出BE=4,设半径为x,得出OE=x-3,然后根据Rt△BOE 的勾股定理求出x的值,从而得出AB的长度.
试题解析:(1)、∵AB是半圆O的直径,
∴∠C=90°,
∵OD∥AC,
∴∠OEB=∠C=90°,
∴OD⊥BC,
∴BE=CE,
∴E为BC的中点;
(2)、设圆的半径为x,则OB=OD=x,OE=x﹣3,
∵BE=![]() BC=4,
BC=4,
在Rt△BOE中,OB2=BE2+OE2,
∴x2=42+(x﹣3)2,解得![]() ,
,
∴AB=2x=![]() .
.


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
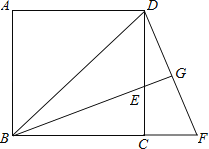
(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
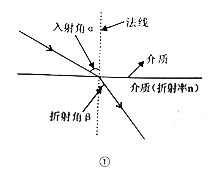
【题目】光线从空气射入水中会发生折射现象,发生折射时,满足的折射定律如图①所示:折射率![]() (
(![]() 代表入射角,
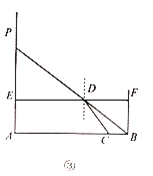
代表入射角,![]() 代表折射角).小明为了观察光线的折射现象,设计了图②所示的实验;通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块,图③是实验的示意图,点A,C,B在同一直线上,测得
代表折射角).小明为了观察光线的折射现象,设计了图②所示的实验;通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块,图③是实验的示意图,点A,C,B在同一直线上,测得![]() ,则光线从空射入水中的折射率n等于________.
,则光线从空射入水中的折射率n等于________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E,![]() .作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
.作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
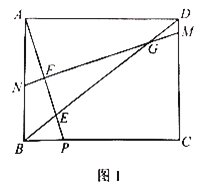
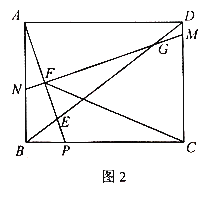
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() .
.
(3)如图2,在(2)的条件下,连接CF,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
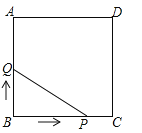
A.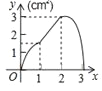 B.
B.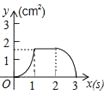 C.
C.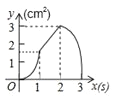 D.
D.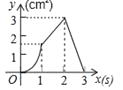
查看答案和解析>>
科目:初中数学 来源: 题型:
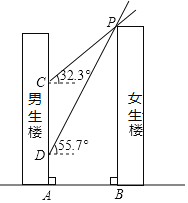
【题目】如图,男生楼在女生楼的左侧,两楼高度均为90m,楼间距为AB,冬至日正午,太阳光线与水平面所成的角为![]() ,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为
,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为![]() ,女生楼在男生楼墙面上的影高为DA,已知
,女生楼在男生楼墙面上的影高为DA,已知![]() .
.
![]() 求楼间距AB;
求楼间距AB;
![]() 若男生楼共30层,层高均为3m,请通过计算说明多少层以下会受到挡光的影响?
若男生楼共30层,层高均为3m,请通过计算说明多少层以下会受到挡光的影响?![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
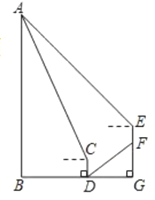
【题目】小明同学上周末对公园钟楼(AB)的高度进行了测量,如图,他站在点D处测得钟楼顶部点A的仰角为67°,然后他从点D沿着坡度为i=1:![]() 的斜坡DF方向走20米到达点F,此时测得建筑物顶部点A的仰角为45°.已知该同学的视线距地面高度为1.6米(即CD=EF=1.6米),图中所有的点均在同一平面内,点B、D、G在同一条直线上,点E、F、G在同一条直线上,AB、CD、EF均垂直于BG.则钟楼AB的高约为?(精确到0.1)(参考数据:sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)
的斜坡DF方向走20米到达点F,此时测得建筑物顶部点A的仰角为45°.已知该同学的视线距地面高度为1.6米(即CD=EF=1.6米),图中所有的点均在同一平面内,点B、D、G在同一条直线上,点E、F、G在同一条直线上,AB、CD、EF均垂直于BG.则钟楼AB的高约为?(精确到0.1)(参考数据:sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生“第二课堂“活动的选修情况,对报名参加A.跆拳道,B.声乐,C.足球,D.古典舞这四项选修活动的学生(每人必选且只能选修一项)进行抽样调查.并根据收集的数据绘制了图①和图②两幅不完整的统计图.

根据图中提供的信息,解答下列问题:
(1)本次调查的学生共有 人;在扇形统计图中,B所对应的扇形的圆心角的度数是 ;
(2)将条形统计图补充完整;
(3)在被调查选修古典舞的学生中有4名团员,其中有1名男生和3名女生,学校想从这4人中任选2人进行古典舞表演.请用列表或画树状图的方法求被选中的2人恰好是1男1女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com