练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】（2017湖南株洲）如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点（Brocard point）是法国数学家和数学教育家克洛尔（A．L．Crelle 1780﹣1855）于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡（Brocard 1845﹣1922）重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=（ ）

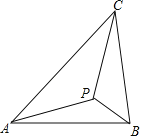
    A. 5 B. 4 C. 3+ D. 2+

    【答案】D

    【解析】

    如图，在等腰直角三角形△DEF中，∠EDF=90°，DE=DF，∠1=∠2=∠3，

    ∵∠1+∠QEF=∠3+∠DFQ=45°，∴∠QEF=∠DFQ，∵∠2=∠3，

    ∴△DQF∽△FQE，∴，

    ∵DQ=1，∴FQ=，EQ=2，∴EQ+FQ=2+，

    故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，是的垂直平分线上一点，是轴上一点且.

    （1）若，，求点的坐标；

    （2）在（1）的条件下，求证：；

    （3）如图2，已知，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，在△ABC中，∠A＜90°，P是BC边上的一点，P1，P2是点P关于AB、AC的对称点，连结P1P2，分别交AB、AC于点D、E．

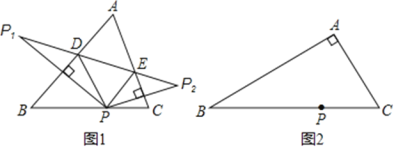
    （1）若∠A＝52°，求∠DPE的度数；

    （2）如图2，在△ABC中，若∠BAC＝90°，用三角板作出点P关于AB、AC的对称点P1、P2，（不写作法，保留作图痕迹），试判断点P1，P2与点A是否在同一直线上，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：在平面直角坐标系中，若两点P、Q的坐标分别是P（x1，y1）、

    Q（x2，y2），则P、Q这两点间的距离为|PQ|=．如P（1，2），Q（3，4），则|PQ|==2．

    对于某种几何图形给出如下定义：符合一定条件的动点形成的图形，叫做符合这个条件的点的轨迹．如平面内到线段两个端点距离相等的点的轨迹是这条线段的垂直平分线．

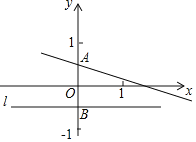
    解决问题：如图，已知在平面直角坐标系xOy中，直线y=kx+交y轴于点A，点A关于x轴的对称点为点B，过点B作直线l平行于x轴．

    （1）到点A的距离等于线段AB长度的点的轨迹是　 　；

    （2）若动点C（x，y）满足到直线l的距离等于线段CA的长度，求动点C轨迹的函数表达式；

    问题拓展：（3）若（2）中的动点C的轨迹与直线y=kx+交于E、F两点，分别过E、F作直线l的垂线，垂足分别是M、N，求证：①EF是△AMN外接圆的切线；②为定值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图, 在△DAE中, ∠DAE＝40°, B、C两点在直线DE上，且∠BAE＝∠BEA，∠CAD＝∠CDA，则∠BAC的大小是（　　）

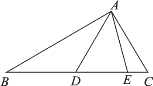
    A.100°B.90°C.80°D.120°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF=∠GAC．

    （1）求证：△ADE∽△ABC；

    （2）若AD=3，AB=5，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB=AC，AE=AF，BE与CF交于点D，则①△ABE≌△ACF；②△BDF≌△CDE；③D在∠BAC的平分线上，以上结论中，正确的是

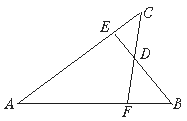
    A. 只有①B. 只有②

    C. 只有①和②D. ①②与③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC=12cm，BC=9cm，点D为AB的中点．

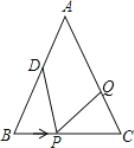
    （1）如果点P在线段BC上以3厘米/秒的速度由B向C点运动，同时点Q在线段CA上由C点向A点运动．

    ①若点Q的运动速度与点P的运动速度相等，当经过1秒时，△BPD与△CQP是否全等，请判断并说明理由；

    ②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD≌△CPQ？

    （2）若点Q以②的运动速度从点C出发，点P以原来运动速度从点B同时出发，都逆时针沿△ABC的三边运动，求经过多长时间，点P与点Q第一次在△ABC的哪条边上会相遇？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E。

    （1）①求证图1中△ADC≌△CEB；②证明DE=AD+BE；

    （2）当直线MN绕点C旋转到图2的位置时，请说明DE=AD－BE的理由；

    （3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE又具有怎样的等量关系?请直接写出这个等量关系（不必说明理由）。

    查看答案和解析>>

    同步练习册答案