Question

如图所示，点A，F，C，D在同一直线上，点B和点E分别在直线AD的两侧，且AB=DE，∠A=∠D，AF=DC．
 
（1）求证：四边形BCEF是平行四边形；
（2）若∠ABC=90°，AB=4，BC=3，当AF为何值时，四边形BCEF是菱形．

Answer 1

（1）由AF=DC可得AC=DF，再有AB=DE，∠A=∠D即可证得△ABC≌DEF，即得BC=EF，∠ACB=∠DFE，则可得BC∥EF，从而证得四边形BCEF是平行四边形；（2）

解析试题分析：（1）由AF=DC可得AC=DF，再有AB=DE，∠A=∠D即可证得△ABC≌DEF，即得BC=EF，∠ACB=∠DFE，则可得BC∥EF，从而证得四边形BCEF是平行四边形；
（2）连接BE，交CF与点G，由四边形BCEF是平行四边形，可知当BE⊥CF时，四边形BCEF是菱形，先根据勾股定理求得AC的长，证得△ABC∽△BGC，根据相似三角形的性质可得CG的长，从而可以求得结果.
（1）∵AF=DC，
∴AF+FC=DC+FC，即AC=DF
在△ABC和△DEF中，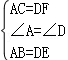
，
∴△ABC≌DEF（SAS），
∴BC=EF，∠ACB=∠DFE，
∴BC∥EF，
∴四边形BCEF是平行四边形；
（2）连接BE，交CF与点G，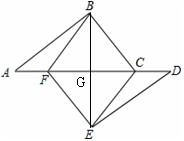

∵四边形BCEF是平行四边形，
∴当BE⊥CF时，四边形BCEF是菱形，
∵∠ABC=90°，AB=4，BC=3，
∴AC=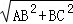=5，
∵∠BGC=∠ABC=90°，∠ACB=∠BCG，
∴△ABC∽△BGC，
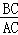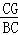∴=，即=，
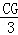∴CG=，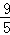
∵FG=CG，
∴FC=2CG=，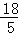
∴AF=AC﹣FC=5﹣=，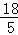
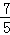∴当AF=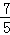时，四边形BCEF是菱形．
考点：全等三角形的判定和性质，平行四边形、菱形的判定和性质，勾股定理，相似三角形的判定和性质
点评：特殊四边形的判定和性质的应用是初中数学极为重要的知识，贯穿于整个初中数学的学习，与各个知识点联系极为容易，是中考的热点.