
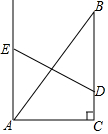
 如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=4,点D在BC上,以AB为对角线的所有平行四边形ADBE中,DE的最小值是3.
如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=4,点D在BC上,以AB为对角线的所有平行四边形ADBE中,DE的最小值是3.  中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:解答题
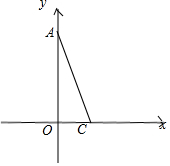 如图,△ABC在平面坐标系内,点A(0,3$\sqrt{3}$),C(2,0).点B为y轴上动点,求$\frac{1}{2}$AB+BC的最小值.
如图,△ABC在平面坐标系内,点A(0,3$\sqrt{3}$),C(2,0).点B为y轴上动点,求$\frac{1}{2}$AB+BC的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
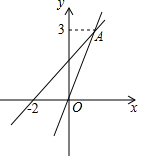 已知正比例函数y=mx与一次函数y=ax+b的图象交于点A(1,3);
已知正比例函数y=mx与一次函数y=ax+b的图象交于点A(1,3);查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
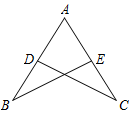 如图,点D、E分别在线段AB、AC上,联结BE,CD,BE=CD,要使△ABE≌△ACD,还需添加一个条件,这个条件可以是∠B=∠C(答案不唯一) (只要写一个条件).
如图,点D、E分别在线段AB、AC上,联结BE,CD,BE=CD,要使△ABE≌△ACD,还需添加一个条件,这个条件可以是∠B=∠C(答案不唯一) (只要写一个条件).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
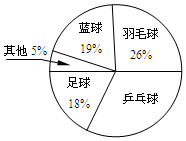 闵行区某校对六年级新生第一学期体育选修课的情况作了全面调查.结果如图.根据如图解答下列问题:
闵行区某校对六年级新生第一学期体育选修课的情况作了全面调查.结果如图.根据如图解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com