如图所示.在Rt△ABC中.∠B=90°.AC=100cm.∠A=60°.点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动.同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动.当其中一个点到达终点时.另一个点也随之停止运动．设点D.E运动的时间是t秒．过点D作DF⊥BC于点F.连接DE.EF．(1)求证:四边形AEFD是平行四边形,(2)四边形AEFD能够� 题目和参考答案——青夏教育精英家教网—

6．

如图所示，在Rt△ABC中，∠B=90°，AC=100cm，∠A=60°，点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤25）．过点D作DF⊥BC于点F，连接DE，EF．
（1）求证：四边形AEFD是平行四边形；
（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；
（3）当t为何值时，△DEF为直角三角形？请说明理由．

分析（1）根据时间和速度表示出AE和CD的长，利用30°所对的直角边等于斜边的一半求出DF的长为4t，则AE=DF，再证明，AE∥DF即可解决问题．
（2）根据（1）的结论可以证明四边形AEFD为平行四边形，如果四边形AEFD能够成为菱形，则必有邻边相等，则AE=AD，列方程求出即可；
（3）当△DEF为直角三角形时，有三种情况：①当∠EDF=90°时，如图3，②当∠DEF=90°时，如图4，
③当∠DFE=90°不成立；分别找一等量关系列方程可以求出t的值．

解答证明：（1）由题意得：AE=2t，CD=4t，
∵DF⊥BC，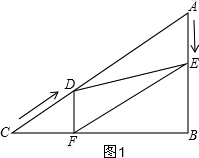
∴∠CFD=90°，
∵∠C=30°，
∴DF=$\frac{1}{2}$CD=$\frac{1}{2}$×4t=2t，
∴AE=DF；
∵DF⊥BC，
∴∠CFD=∠B=90°，
∴DF∥AE，
∴四边形AEFD是平行四边形．

（2）四边形AEFD能够成为菱形，理由是：
由（1）得：AE=DF，
∵∠DFC=∠B=90°，
∴AE∥DF，
∴四边形AEFD为平行四边形，
若?AEFD为菱形，则AE=AD，
∵AC=100，CD=4t，
∴AD=100-4t，
∴2t=100-4t，
t=$\frac{50}{3}$，
∴当t=$\frac{50}{3}$时，四边形AEFD能够成为菱形；

（3）分三种情况：
①当∠EDF=90°时，如图3，
则四边形DFBE为矩形，
∴DF=BE=2t，
∵AB=$\frac{1}{2}$AC=50，AE=2t，
∴2t=50-2t，
t=$\frac{25}{2}$，
②当∠DEF=90°时，如图4，
∵四边形AEFD为平行四边形，
∴EF∥AD，
∴∠ADE=∠DEF=90°，
在Rt△ADE中，∠A=60°，AE=2t，
∴AD=t，
∴AC=AD+CD，
则100=t+4t，
t=20，
③当∠DFE=90°不成立；
综上所述：当t为$\frac{25}{2}$或20时，△DEF为直角三角形．

点评本题是四边形的综合题，考查了平行四边形、菱形、矩形的性质和判定，也是运动型问题，难度不大，是常出题型；首先要表示出两个动点在时间t时的路程，弄清动点的运动路径，再根据其运动所形成的特殊图形列式计算；同时，所构成的直角三角形因为直角顶点不确定，所以要分情况进行讨论．

练习册系列答案

单元测试AB卷吉林出版集团有限责任公司系列答案

小学语文词语手册开明出版社系列答案