

 ∠MBC,∠PCB=
∠MBC,∠PCB= ∠NCB
∠NCB ∠MBC+
∠MBC+ ∠NCB=
∠NCB= (180°-α)=90°-
(180°-α)=90°- α
α α)=90°+
α)=90°+ α
α ∠MBC=
∠MBC= (α+β)
(α+β) α,∠MBP=∠BAP+∠APB
α,∠MBP=∠BAP+∠APB (α+β)-
(α+β)- α=
α= β;
β;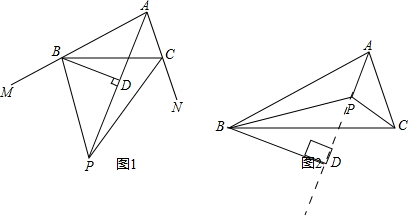
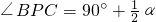 ;
;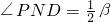 .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•松江区模拟)如图,已知在△ABC中,AC=BC,将△ABC绕点C顺时针旋转到△DEC,其中点A运动到点D,点B运动到点E,记旋转角为α,∠B=β,如果AD∥BC,那么α与β的数量关系为
(2013•松江区模拟)如图,已知在△ABC中,AC=BC,将△ABC绕点C顺时针旋转到△DEC,其中点A运动到点D,点B运动到点E,记旋转角为α,∠B=β,如果AD∥BC,那么α与β的数量关系为查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•定海区模拟)如图,已知Rt△ABC中,AC=b,BC=a,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn为( )
(2013•定海区模拟)如图,已知Rt△ABC中,AC=b,BC=a,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn为( )查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com