练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    (1)由图可以看出，每隔13年全世界人口增加_____亿．

    (2)全世界人口每年大约增加多少亿？

    (3)在1974年和2000年之间，怎样用年份数表示当年的人口？

    (4)在哪一年全世界的人口达到55亿？

    (5)假如以后仍按这样的速度增长，到哪一年全世界的人口就会超过80亿？

    答案：
    解析：

    条型统计图也能直观地反映两个数量之间的关系

    (1)10亿．

    (2)10÷13≈0.7692，故全世界人口每年大约增加0.7692亿

    (3)按每年约增0.7692亿人口算出1974年以后各年的人口约数，然后列表表示当年的人口，如

    (4)由图知1987年人口达到50亿，设再x年世界人口达到55亿，则由50＋0.7692x=55可求得x≈7(年)，即1994年全世界的人口达到了55亿．

    (5)由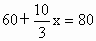，得x=26(年)因此，假如以后仍按这样的速度增长，到2027年全世界人口就会超过80亿．


    提示：

    ①由于每隔13年，全世界人口增加数相同，所以每年人口增加数应等于13年人口增加数除以年份数(13)年．

    ②若设从1987年再过x年全世界人口达到55亿，可列方程：50＋年增长数x=55求得．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    14、解方程|x-1|+|x+2|=5．由绝对值的几何意义知，该方程表示求在数轴上与1和-2的距离之和为5的点对应的x的值．在数轴上，1和-2的距离为3，满足方程的x对应点在1的右边或-2的左边，若x对应点在1的右边，由图可以看出x=2；同理，若x对应点在-2的左边，可得x=-3，故原方程的解是x=2或x=-3．

    参考阅读材料，解答下列问题：
    （1）方程|x+3|=4的解为
    1和-7
    ．
    （2）解不等式|x-3|+|x+4|≥9；
    （3）若|x-3|+|x+4|≤a对任意的x都成立，求a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    24、一个点从数轴原点开始，先向右移动3个单位长度，再向右移动2个单位长度，如图所示，由图可以看出，到达的终点是表示5的点．
    （1）画图表示一个点从数轴上的原点开始按下列方式移动到达的终点，并说明它们表示的是什么数的点．
    ①向左移动2个单位，再向左移动个4单位长度；
    ②向左移动2个单位，再向右移动个5单位长度；
    ③向右移动4个单位，再向左移动个5单位长度；
    （2）将上述①、②和③中移动到达终点表示的数，用“＜”连接起来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    为了迎接“2008北京奥运”，实验中学举行了一次“奥运知识竞赛”，共有900名学生参正整数，满分为100分）进行统计．请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题：
    （1）填充频率颁表中的空格；
    （2）补全频率分布直方图；
    （3）全体参赛学生中，竞赛成绩落在哪组范围内的人数最多？
    答：
    由图可以看出80.5-90.5的学生人数最多
    由图可以看出80.5-90.5的学生人数最多
    ．
    （4）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？
    频率分布表
      分组 频数 频率
    50.5-60.5  4 0.08
    60.5-70.5  8 0.16
    70.5-80.5 18 0.20
    80.5-90.5  16 0.32
    90.5-100.5    
      合计    

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离；即，也就是说，|x|表示在数轴上数x与数0对应点之间的距离；

     这个结论可以推广为表示在数轴上，对应点之间的距离；

    例1:解方程，容易看出，在数轴下与原点距离为2点的对应数为±2，即该方程的解为x=±2

    例2:解不等式▏x-1▏＞2，如图，在数轴上找出▏x-1▏=2的解，即到1的距离为2的点对应的数为－1、3，则▏x-1▏＞2的解为x<－1或x>3

    例3:解方程。由绝对值的几何意义知，该方程表示求在数轴上与1

    和－2的距离之和为5的点对应的x的值。在数轴上，1和－2的距离为3，满足方程的x对应点在1的右边或－2的左边，若x对应点在1的右边，由图可以看出x＝2；同理，若x对应点在－2的左边，可得x＝－3，故原方程的解是x=2或x=－3

    参考阅读材料，解答下列问题：

    （1）方程的解为                     

    （2）解不等式≥9；

    （3）若≤a对任意的x都成立，求a的取值范围.

    查看答案和解析>>

    科目：初中数学 来源：2011年广东省佛山市顺德一中中考数学一模试卷（解析版） 题型：解答题

    解方程|x-1|+|x+2|=5．由绝对值的几何意义知，该方程表示求在数轴上与1和-2的距离之和为5的点对应的x的值．在数轴上，1和-2的距离为3，满足方程的x对应点在1的右边或-2的左边，若x对应点在1的右边，由图可以看出x=2；同理，若x对应点在-2的左边，可得x=-3，故原方程的解是x=2或x=-3．

    参考阅读材料，解答下列问题：
    （1）方程|x+3|=4的解为______．
    （2）解不等式|x-3|+|x+4|≥9；
    （3）若|x-3|+|x+4|≥a对任意的x都成立，求a的取值范围．

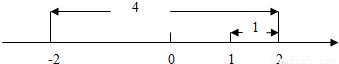
    查看答案和解析>>

    同步练习册答案