
分析 设购买A种树苗x株,则购买B种树苗(8000-x)株,根据它们的成活率和使这批树苗的总成活率不低于80%列出不等式并解答.
解答 解:设购买A种树苗x株,则购买B种树苗(800-x)株,
依题意得:70% x+85%(8000-x)≥8000×80%,
70 x+85(8000-x)≥800×80,
70x+680000-85x≥640000,
-15x≥-40000,
x≤2666$\frac{2}{3}$.
∵x是正整数,
∴x=26667.
答:A种树苗最多可以购买26667株.
点评 本题考查了一元一次不等式解实际问题的运用,解决问题的关键是读懂题意,找到关键描述语,找到所求的量的等量关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD.
如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
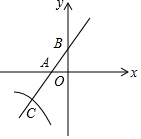 如图,已知一次函数${y}_{1}=\frac{4}{3}x+4$的图象分别交x轴于A、B两点,交反比例函数y2=$\frac{a}{x}$(x<0)的图象于第三象限的C点,且AB=AC.
如图,已知一次函数${y}_{1}=\frac{4}{3}x+4$的图象分别交x轴于A、B两点,交反比例函数y2=$\frac{a}{x}$(x<0)的图象于第三象限的C点,且AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com