Question

17．如图，在△ABC中，AB=AC=5，BC=8，点D是边BC上一动点（不与B，C重合），E是AC上一个动点，始终保持∠ADE=∠B，则当△DCE为直角三角形时，BD的长为4或$\frac{25}{4}$．

Answer 1

分析 因为∠C为定角，D、E为动点，所以△DCE为直角三角形有两种情况：
①当∠DEC=90°时，△DCE为直角三角形，如图1，根据等腰三角形三线合一的性质求出BD的长；
②当∠EDC=90°时，△DCE为直角三角形，如图2，作辅助线，根据外角定理和△BFA∽△BAD求出BD的长．

解答 解：分两种情况：
①当∠DEC=90°时，△DCE为直角三角形，如图1，
∴∠AED=90°，
∵AB=AC，
∴∠B=∠C，
∵∠ADE=∠B，
∴∠ADE=∠C，
∵∠DAE=∠DAC，
∴△ADE∽△ACD，
∴∠ADC=∠AED=90°，
∴AD⊥BC，
∴BD=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4；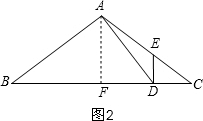
②当∠EDC=90°时，△DCE为直角三角形，如图2，
过A作AF⊥BC于F，则BF=4，
∵∠ADE+∠EDC=∠B+∠BAD，
∠ADE=∠B，
∴∠EDC=∠BAD=90°，
∴∠BAD=∠BFA=90°，
∵∠B=∠B，
∴△BFA∽△BAD，
∴$\frac{AB}{BD}=\frac{BF}{AB}$，
∵AB=5，
∴$\frac{5}{BD}=\frac{4}{5}$，
∴BD=$\frac{25}{4}$，
综上所述，BD为4或$\frac{25}{4}$，
故答案为：4或$\frac{25}{4}$．

点评 本题考查了等腰三角形、相似三角形的性质和判定，明确等边对等角和等角对等边，相似三角形常用的判定是：两角对应相等的两个三角形相似，在几何证明中常利用相似得比例式求边的长度；同时又运用了外角定理求角相等；本题还运用了分类讨论的思想，尤其动点形成的三角形是直角三角形或等腰三角形时，要根据具体问题分情况进行讨论．