
���� ��1�����ݷ�ĸ�������ķ������Խ���⣻
��2��������Ŀ�е����ӿ��������ν���⣮
��� �⣺��1��$\frac{1}{{\sqrt{3}+1}}+\frac{1}{{\sqrt{5}+\sqrt{3}}}+\frac{1}{{\sqrt{7}+\sqrt{5}}}+��+\frac{1}{{\sqrt{121}+\sqrt{119}}}$
=$\frac{1}{2}$��$\sqrt{3}$-1��+$\frac{1}{2}$��$\sqrt{5}$-$\sqrt{3}$��+$\frac{1}{2}$��$\sqrt{7}$-$\sqrt{5}$��+��+$\frac{1}{2}$��$\sqrt{121}$-$\sqrt{119}$����
=$\frac{1}{2}$��$\sqrt{121}$-1����
=$\frac{1}{2}$��11-1����
=5��
��2���١�a=$\frac{1}{{\sqrt{2}-1}}$=$\frac{\sqrt{2}+1}{��\sqrt{2}-1����\sqrt{2}+1��}$=$\sqrt{2}$+1��
��a-1=$\sqrt{2}$��
�ࣨa-1��2=2����a2-2a=1��
��4a2-8a+1=4��a2-2a��+1=4��1+1=5��
�ڡ�a=$\frac{1}{{\sqrt{2}-1}}$=$\frac{\sqrt{2}+1}{��\sqrt{2}-1����\sqrt{2}+1��}$=$\sqrt{2}$+1��
��a-1=$\sqrt{2}$��
�ࣨa-1��2=2����a2-2a=1��
��a3-3a2+a+1
=a��a2-2a��-a2+a+1
=a-a2+a+1
=-a2+2a+1
=-��a2-2a��+1
=-1+1
=0��
�ʴ�Ϊ��0��
���� ���⿼����θ�ʽ�Ļ�����ֵ�������Ĺؼ�����ȷ���θ�ʽ������ֵ�ķ�����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
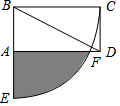 ��ͼ����֪����ABCD�У�AB=1 cm��BC=2 cm����BΪԲ�ģ�BCΪ�뾶��$\frac{1}{4}$Բ����AD�ڵ�F����BA���ӳ����ڵ�E��������BCE����������ʣ�ಿ�ֵ����Ϊ$\frac{2}{3}$��-$\frac{\sqrt{3}}{2}$��
��ͼ����֪����ABCD�У�AB=1 cm��BC=2 cm����BΪԲ�ģ�BCΪ�뾶��$\frac{1}{4}$Բ����AD�ڵ�F����BA���ӳ����ڵ�E��������BCE����������ʣ�ಿ�ֵ����Ϊ$\frac{2}{3}$��-$\frac{\sqrt{3}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����ߺ�һ�Ƕ�Ӧ��ȵ�����������ȫ�� | |
| B�� | ��ֱ��ͬһ��ֱ�ߵ���ֱ��ƽ�� | |
| C�� | �ڴ������ | |
| D�� | ��һ������60��ĵ����������ǵȱ������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
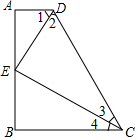 ��ͼ��BC��AB��CEƽ�֡�BCD��DEƽ�֡�ADC����2+��3=90�㣬���ж�AD��AB��λ�ù�ϵ����˵�����ɣ�
��ͼ��BC��AB��CEƽ�֡�BCD��DEƽ�֡�ADC����2+��3=90�㣬���ж�AD��AB��λ�ù�ϵ����˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com