
 如图,矩形ABCD与菱形EFGH的对角线均交于点O,且EG∥BC,将矩形折叠,使点C与点O重合,折痕MN恰好过点G若AB=$\sqrt{6}$,EF=2,∠H=120°,则DN的长为( )
如图,矩形ABCD与菱形EFGH的对角线均交于点O,且EG∥BC,将矩形折叠,使点C与点O重合,折痕MN恰好过点G若AB=$\sqrt{6}$,EF=2,∠H=120°,则DN的长为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{3}}{2}$ | C. | $\sqrt{6}$-$\sqrt{3}$ | D. | 2$\sqrt{3}$-$\sqrt{6}$ |
分析 延长EG交DC于P点,连接GC、FH,则△GCP为直角三角形,证明四边形OGCM为菱形,则可证CG=OM=CM=OG=$\sqrt{3}$,由勾股定理求得GP的值,再由梯形的中位线定理CM+DN=2GP,即可得出答案.
解答 解: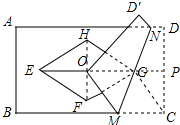 延长EG交DC于P点,连接GC、FH;如图所示:
延长EG交DC于P点,连接GC、FH;如图所示:
则CP=DP=$\frac{1}{2}$CD=$\frac{\sqrt{6}}{2}$,△GCP为直角三角形,
∵四边形EFGH是菱形,∠EHG=120°,
∴GH=EF=2,∠OHG=60°,EG⊥FH,
∴OG=GH•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
由折叠的性质得:CG=OG=$\sqrt{3}$,OM=CM,∠MOG=∠MCG,
∴PG=$\sqrt{C{G}^{2}-C{P}^{2}}$=$\frac{\sqrt{6}}{2}$,
∵OG∥CM,
∴∠MOG+∠OMC=180°,
∴∠MCG+∠OMC=180°,
∴OM∥CG,
∴四边形OGCM为平行四边形,
∵OM=CM,
∴四边形OGCM为菱形,
∴CM=OG=$\sqrt{3}$,
根据题意得:PG是梯形MCDN的中位线,
∴DN+CM=2PG=$\sqrt{6}$,
∴DN=$\sqrt{6}$-$\sqrt{3}$;
故选:C.
点评 本题考查了矩形的性质、菱形的性质、翻折变换的性质、勾股定理、梯形中位线定理、三角函数等知识;熟练掌握菱形和矩形的性质,由梯形中位线定理得出结果是解决问题的关键.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | a2•a3=a6 | B. | (3ab2)3=9a3b6 | C. | (a2b)3÷(-ab)2=a4b | D. | (a-2)2=a2-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 根据卫生防疫部门要求,游泳池必须定期换水,清洗.某游泳池周五早上8:00打开排水孔开始排水,排水孔的排水速度保持不变,期间因清洗游泳池需要暂停排水,游泳池的水在11:30全部排完.游泳池内的水量Q(m3)和开始排水后的时间t(h)之间的函数图象如图所示,根据图象解答下列问题:
根据卫生防疫部门要求,游泳池必须定期换水,清洗.某游泳池周五早上8:00打开排水孔开始排水,排水孔的排水速度保持不变,期间因清洗游泳池需要暂停排水,游泳池的水在11:30全部排完.游泳池内的水量Q(m3)和开始排水后的时间t(h)之间的函数图象如图所示,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3+$\sqrt{3}$=3$\sqrt{3}$ | B. | $\sqrt{{{(-2)}^2}}$=2 | C. | $\sqrt{50}$=$\sqrt{25+25}$=5+5=10 | D. | $\sqrt{4\frac{1}{9}}$=2$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
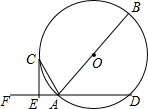 如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.
如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com